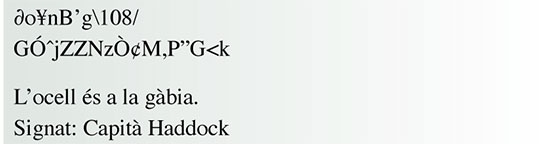La implantació de les noves tecnologies comporta un seguit de canvis significatius en els nostres usos i costums. Un d’ells afecta l’art de signar. Internet ofereix la possibilitat de signar documents sense la presència física de les persones implicades. Però, perquè aquest tipus de signatures siguin reconegudes, cal que es realitzin amb garanties. Les signatures digitals plantegen problemes legals, científics i tècnics dignes de consideració. En aquest article comentem alguns aspectes de la base matemàtica que els és inherent.
«La signatura electrònica és un conjunt de caràcters que s’afegeixen a un document electrònic i que permeten autentificar la identitat del “signatari”»
Per il·lustrar un dels protocols més emprats en les signatures electròniques hem elaborat un petit relat protagonitzat per dos personatges de ficció: Tintín i el capità Haddock. Tintín rep un missatge misteriós, xifrat i signat per Haddock; per esbrinar si la signatura és autèntica recorrerà als coneixements del professor Tornassol. L’episodi no és extret de cap de les populars narracions d’Hergé, però sí que ho és el contingut del missatge; de ben segur que els seguidors d’aquest heroi no tindran cap dificultat per identificar-lo.

El DNI electrònic serà una targeta que portarà un xip amb informació digital. Entre altres dades identificadores de caràcter personal, el xip inclourà un certificat electrònic, per autentificar la identitat del ciutadà; un certificat electrònic reconegut, per emetre signatures electròniques reconegudes, i claus criptogràfiques per l’emisió i verificació de les signatures.
Signatures electròniques, d’acord amb la Llei
El 17 de setembre de 1999, el Consell de Ministres aprovà el Reial Decret Llei 14/1999 sobre signatura electrònica (BOE 224/ 1999, de 18 de setembre). El 20 de juny de 2003, un Projecte de Llei de signatura electrònica fou publicat en el BOCG 158-1. El 19 de desembre de 2003, s’aprovava la Llei 59/2003 sobre signatura electrònica (BOE 304/2003, de 20 de desembre). El 13 de febrer de 2004, el Consell de Ministres donà llum verda al DNI electrònic, la implantació del qual s’iniciarà aquest any.
Òbviament, sota el nom signatura electrònica no es contempla el fet d’escriure el nostre nom a la fi d’un missatge electrònic, acte que està mancat de tot valor legal. La signatura electrònica és un conjunt de caràcters que s’afegeixen a un document electrònic i que permeten autentificar la identitat del signatari. El signatari és una persona física, que pot actuar en nom propi o en nom d’una persona física o jurídica a la qual representa.
La llei distingeix entre signatura electrònica i signatura electrònica reconeguda. La signatura electrònica reconeguda és la signatura electrònica basada en un certificat electrònic reconegut; té el mateix valor legal que la signatura manuscrita. Els certificats electrònics reconeguts són documents signats electrònicament que han de complir una sèrie de requisits. Permeten: (I) l’autentificació de les parts, és a dir, que l’emissor i el receptor del missatge són qui realment diuen ser; (II) garantir la integritat del missatge; és a dir, que aquest no és alterat després de ser signat; (III) garantir la confidencialitat del missatge; és a dir, que només l’emissor i el receptor hi tenen accés; (IV) garantir la irrefutabilitat del missatge; és a dir, que el signatari no en pugui negar l’autoria.
En l’emissió d’una signatura electrònica la llei contempla, a més, el prestador de serveis de certificació i els dispositius de creació i verificació de la signatura.
El prestador de serveis de certificació és una persona física o jurídica que expedeix certificats electrònics als signataris i els presta el suport necessari en relació a la signatura electrònica. Els certificats electrònics donen fe de la identitat dels usuaris i poden proporcionar, a més, les eines de signatura electrònica. Els dispositius físics de creació de signatures poden variar d’uns casos a altres; es poden utilitzar targetes intel·ligents, màquines lectores, CD, PIN, etc. L’entitat prestadora de serveis facilita el software necessari per a la creació i verificació de les signatures (generalment via Internet), de manera que l’usuari pugui quedar al marge dels aspectes tècnics.
El DNI electrònic
El suport del DNI electrònic serà una targeta de la mateixa mesura que les actuals. L’anvers portarà un xip amb informació digital. Entre altres dades identificadores de caràcter personal, el xip inclourà un certificat electrònic, per autentificar la identitat del ciutadà; un certificat electrònic reconegut, per emetre signatures electròniques reconegudes, i claus criptogràfiques per a l’emissió i verificació de les signatures. Es preveu que es constituirà una autoritat de certificació electrònica personalitzada en el Ministeri de l’Interior, a través de la Direcció General de Policia. La implantació del DNI electrònic serà gradual els propers anys.
Explicarem tot seguit, per mitjà d’un exemple, els aspectes matemàtics que possibiliten l’existència de signatures electròniques digitals.
Digitalització de missatges
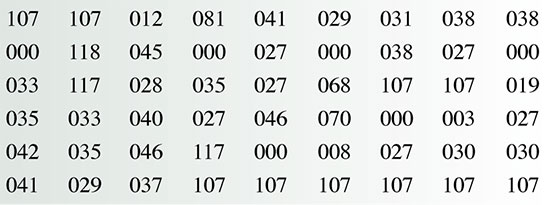
Suposem que volem enviar un text a través de la xarxa, escrit amb caràcters del nostre alfabet (lletres i nombres). A fi que sigui transmissible telemàticament, cal començar reconvertint el seu contingut en una successió de zeros i uns; és a dir, hem de codificar el text en un missatge binari. La taula 1 ofereix un text X codificat en el sistema de numeració binari. La taula 2 ofereix el mateix text codificat en el sistema de numeració decimal. En aquesta exposició, utilitzarem la representació decimal dels nombres per fer els càlculs més fàcils de seguir i perquè les taules ens ocupin menys espai.
La codificació d’un missatge alfabètic en un missatge numèric es coneix com a digitalització. La simple digitalització dels missatges no proporciona cap tipus de confidencialitat enfront de tercers. En principi, se suposa que tots els usuaris d’una xarxa són capaços de codificar un missatge alfabètic en un missatge digital i de descodificar un missatge digital en un missatge alfabètic. El diccionari més generalment emprat per a tal fi és l’anomenat codi ASCII (American Standard Code for Information Interchange), accessible per Internet. En els exemples de les taules 1 i 2 s’ha emprat un codi de 149 caràcters similar a l’ASCII, però una mica simplificat.
Connexions segures
Per aconseguir que la transmissió per xarxa d’un missatge digitalitzat x sigui confidencial es recorre a la criptografia o escriptura secreta. Donat un text accessible per a tothom (text clar), la criptografia s’encarrega de transformar-lo en un criptograma, o text inaccessible per als adversaris. La transformació de missatges clars en criptogrames i viceversa es porta a terme mitjançant claus criptogràfiques, que poden ser molt diverses.
Al llarg dels temps, la criptografia ha estat emprada primordialment per governs i societats secretes. Amb la introducció de les noves tecnologies, aquest art mil·lenari ha experimentat canvis significatius i el seu ús es va generalitzant. Cada cop més sovint, les nostres dades i els nostres pagaments viatgen xifrats per la xarxa.
Per xifrar els missatges electrònics hi ha diversos protocols. Mitjançant programes informàtics, aquests protocols efectuen operacions aritmètiques en un missatge digitalitzat, amb el propòsit d’amagar-ne el contingut. El missatge digitalitzat es transforma així en un missatge digital xifrat, que és el que viatja.
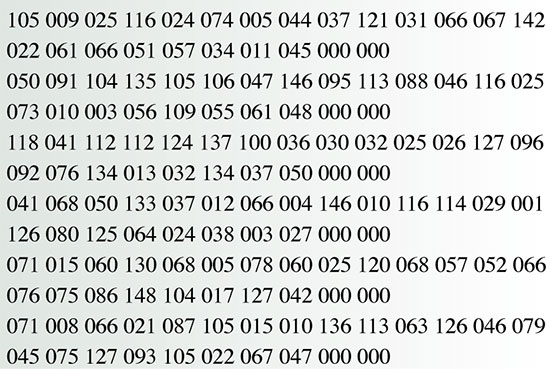
La taula 3 conté un missatge y obtingut xifrant el missatge x de la taula 2. Descodificant y obtindríem un criptograma del missatge X, totalment incomprensible.
Criptografia de clau pública; criptografia de clau privada
El desenvolupament de la criptografia ha conegut dues etapes ben diferenciades: abans de l’any 1975, dita l’etapa clàssica, i a partir d’aquesta data, en què s’inicià la criptografia de clau pública o asimètrica.
La criptografia clàssica empra uns protocols en què l’emissor i el receptor d’un missatge acorden prèviament la clau. La informació continguda en la clau serveix tant per a xifrar el missatge com per a desxifrar-lo. La transmissió de les claus sol estar en mans d’agents especials; les claus s’apleguen en llibres de codis o similars (que són sempre font de problemes).
La criptografia de clau pública neix l’any 1976 per mà de W. Diffie i M. E. Hellman. La proposta de Diffie i Hellman fou la creació d’uns protocols que permetessin deixar a la llum les claus necessàries per a xifrar els missatges i amagar les claus necessàries per a desxifrar-los. Les claus privades serien exclusives de cada usuari. De fet, Diffie i Hellman no sabien com portar a la pràctica la idea de la criptografia de clau asimètrica. Es tractava de construir una mena d’autopistes d’anada, però sense retorn, excepte per a una sola persona (la receptora del missatge).
«La signatura electrònica reconeguda té le mateix valor legal que la signatura manuscrita»
Nombres primers secrets
L’any 1978, R. Rivest, A. Shamir i L. Adleman¹ idearen un protocol per implementar la criptografia de clau pública. La seva proposta fou utilitzar els nombres primers com a dades secretes per a la creació de claus asimètriques. El protocol RSA (Rivest, Shamir i Adleman) segueix l’esquema de Diffie i Hellman: cada usuari té assignada una clau pública i una clau privada. La clau pública consta d’un parell de nombres (n, e), que estan a l’abast de tothom en un directori. El nombre n s’obté multiplicant dos nombres primers: n=p·q. El nombre e s’escull de manera que el màxim comú divisor de e i del nombre (p–1)(q–1) sigui igual a 1. Els nombres primers p, q no es revelen; són una dada exclusiva de la identitat de l’usuari. A partir d’ells es calcula el nombre secret d per la condició que e·d–1 sigui un múltiple de (p–1)(q–1). El parell (n, d) constitueix la clau privada de cada usuari. Com veurem, el coneixement de d serà imprescindible per desxifrar els missatges.²
La asimetria de les claus resulta del fet següent: donats dos nombres primers p, q, és molt fàcil multiplicar-los i obtenir el nombre n. En canvi, donat un nombre n «prou gran» que sigui producte de dos primers p, q de la mateixa mida, es tarda «molt temps» per calcular p, q. Per exemple, descompondre un nombre de 1024 bits (unes 300 xifres decimals) requereix unes 2100 operacions bàsiques en el millor dels algoritmes que avui coneixem. Sense conèixer p, q no se sap calcular d. Per tant, el coneixement d’una clau pública RSA, (n, e), ben construïda i amb n prou gran, no permet avui el càlcul de la clau privada (n, d) associada.
La taula 4 és un directori de claus públiques RSA amb dos usuaris: el reporter Tintín i el capità Haddock.³ El parell (nt, et) és la clau pública de Tintín; el parell (nh, eh) és la clau pública de Haddock. D’acord amb el seu esperit, no mostrem les claus privades ni de Tintín: (nt, dt), ni del capità Haddock: (nh, dh).
El protocol RSA per xifrar missatges digitals
Estem ara en condicions d’explicar el funcionament del protocol RSA; començarem per dir com se xifra un missatge x coneguda la clau pública (n, e) del receptor: es multiplica el missatge x per ell mateix e vegades, realitzant sempre els càlculs mòdul n; el resultat és el missatge xifrat: y = xe mod n. El missatge de la taula 3 s’ha generat a partir del missatge de la taula 2 amb la clau pública de Tintín, de la taula 4. Per calcular-lo, s’ha dividit el missatge de la taula 2 en 6 blocs de 9 xifres en base 149, i s’ha interpretat cada bloc com un nombre més petit que nt. Cada bloc s’ha multiplicat per ell mateix et vegades, reduint sempre els càlculs mòdul nt. Han sorgit així els 6 blocs de 24 xifres en base 149 de la taula 3.
Quan el receptor rep un missatge xifrat y=xe mod n, desconeix el valor de x. Per recuperar-lo ha de calcular l’arrel e del missatge y rebut. Atès que els càlculs es fan mòdul n, aquesta arrel és difícil de calcular, llevat que es coneguin els primers p i q. La recuperació del missatge x, un cop conegut el nombre d, que és el secret de n, es basa en la identitat e√y=x=xe·d mod n , descoberta pel matemàtic Leonhard Euler en el segle XVIII. L’any 1977, el MIT sol·licità la patent del protocol RSA, un fet insòlit en matemàtiques, car era el primer algoritme patentat en la història d’aquesta ciència.
El protocol RSA de signatura digital
L’autenticitat de les signatures autògrafes s’estableix per mitjà d’una anàlisi grafològica. Explicaremara com la criptografia de clau pública fa possible l’emissió i l’autentificació de signatures digitals. La signatura digital és emesa pel signatari amb l’ús de la seva clau privada. L’autenticitat d’una signatura digital pot ser verificada per qualsevol persona amb l’ús de la clau pública del signatari.4 La taula 6 explicita l’esquema de signatura RSA per signar un missatge digital i verificar-ne la signatura.
La taula 7 mostra el missatge x de la taula 2 signat amb la clau privada del capità Haddock.
Tramesa d’informació signada i xifrada: signatures reconegudes
Podem ara combinar el protocol RSA de signatures digitals amb el protocol RSA de xifratge de missatges digitals. Estarem, així, en la situació de l’emissió i verificació del que la llei anomena una signatura electrònica reconeguda. Les taules que segueixen n’ofereixen un exemple.
El gargot que apareix sota el text clar de la taula 10 és la signatura electrònica del missatge. Cal, doncs, verificar-la. Com que això ho pot fer tothom, deixarem que ho faci el professor Tornassol:
Cal descodificar el text obtingut. Si tot és correcte, el text clar apareixerà en segon terme.

“L’ocell és a la gàbia” és un dels missatges xifrats que Hergé fa servir per als còmics de Tintín. Si les seues aventures estigueren ambientades en l’actualitat, de ben segur que Tintín es faria servir de la signatura digital per protegir els seus missatges. / Hergé, 1968, Tintín a Amèrica. Editorial Joventut, Barcelona. Traducció catalana de Joaquim Ventalló.
Qüestions de seguretat
La seguretat del protocol RSA es basa en un desconeixement. En l’actualitat, els algoritmes per descompondre els nombres en factors primers no són prou ràpids quan s’executen en els nostres ordinadors. Així, les claus RSA esdevenen segures quan el nombre n té unes 300 xifres decimals (1024 bits). L’ús d’ordinadors molt més potents, o una millora significativa dels algoritmes de factorització, repercutiria en la inseguretat d’aquestes claus.
En el nostre exemple, els nombres n del directori tenen de l’ordre de 50 xifres decimals. Amb la potència de càlcul actual, les claus del directori són insegures (les del nostre DNI seran molt més grans). Tornassol s’assessora5 i, com a resultat, obté la clau privada de Haddock mitjançant un conegut algoritme de factorització (MPQS). Aquest trenca el nombre nh i deixa al descobert el secret del capità: el nombre dh.
Amb altres paraules, el missatge del capità Haddock podria, molt bé, ser apòcrif. Caldrà, doncs, investigar els coneixements aritmètics i la capacitat de càlcul dels adversaris: Rastapopulos, Peggy, el Sindicat de Gànsters de Chicago, etc.
Amb posterioritat al RSA, s’han dissenyat altres protocols criptogràfics que ofereixen la mateixa seguretat que el RSA amb claus molt més petites. Aquests protocols utilitzen propietats sofisticades dels nombres, estudiades en el decurs dels segles XIX i XX.
Conclusió
Els mètodes actuals de signatures digitals es basen en l’existència de problemes aritmètics, la resolució dels quals comporta massa temps i espai amb els mitjans actuals. Millores en el coneixement teòric dels nombres, o en la potència de càlcul dels ordinadors, poden fer variar el seu grau de seguretat. Les possibles repercussions criptogràfiques dels avenços aritmètics han d’ésser estudiades amb cura i tingudes en compte, en tant que sistemes criptogràfics avui segurs poden deixar de ser-ho en un futur no gaire llunyà.
1. Rivest, R., Shamir, A. i L. Adleman, 1978. «A method for obtaining digital signatures and public-key cryptosystems» in Communications of the ACM, 21 (2): 120-126. (Tornar al text)
2. Es tracta d’un càlcul mòdul m=(p–1)(q–1). En general, en els càlculs mòdul m, cada vegada que s’arriba a m es torna a començar. Per exemple, calculem les hores mòdul 12; així, les 13 h equivalen a la 1 h; i si a les 11 h n’hi sumem tres, obtenim les 2 h, etc. (Tornar al text)
3. Hergé (Georges Rémy): Les aventures de Tintín. Editorial Joventut. Traducció catalana de Joaquim Ventalló. Primera aparició de Tintín: 10 de gener de 1929. (Tornar al text)
4. Prescindim en aquesta exposició de l’ús de funcions resum (hash). (Tornar al text)
5. Travesa, A., 1998, Aritmètica. Col·lecció UB. Edicions Univesitat de Barcelona. (Tornar al text)