|
Un temps després de la lectura de la tesi doctoral, on utilitzava el problema de l’agulla de Buffon com a punt de partida dels resultats que havia obtingut en l’àmbit de la geometria integral, em van recomanar el llibre de Martí Domínguez Les confidències del comte de Buffon. De seguida vaig pensar en com d’afortunat va ser aquest personatge; i és que George Louis Lecrerc (1707-1788), nomenat comte de Buffon per Lluís XV, va viure en una etapa del Segle de les Llums molt brillant i suggerent pel que fa a la ciència i a la filosofia. A més, encara que va ser el gran naturalista d’aquest segle, també es va prodigar en altres branques científiques i, per si fóra poc, la seua obra ha transcendit, però no només la Història Natural, de 36 volums, sinó també un suplement a aquesta obra històrica anomenat «Assaig d’aritmètica moral», on es troba l’origen de les probabilitats geomètriques, primer, i, més tard, de la geometria integral i estocàstica. L’estiu de 2007, més de deu anys després dels fets abans esmentats, vaig conèixer l’autor del llibre sobre Buffon en plenes festes de Vistabella del Maestrat (sens dubte un moment d’altura, no debades parlem del poble més alt del nostre territori). Fruit d’aquesta trobada, amb l’excusa que el 2007 es va celebrar el 300 aniversari del naixement de Buffon, i amb l’ànim de donar a entendre per què un problema com el de l’agulla de Buffon ha transcendit i és conegut per tota la comunitat matemàtica, arran de la influència posterior d’aquest en el desenvolupament de tota una teoria matemàtica dinàmica, que barreja investigació bàsica i aplicada al mateix temps, naix aquest article. El vessant matemàtic de Buffon Sens dubte, influït per la seua època, Buffon va considerar les passions com intrínseques de l’ésser humà i, d’aquestes, va dedicar especial atenció als jocs d’atzar. La part més interessant del seu opuscle «Assaig d’aritmètica moral», des del punt de vista matemàtic, és la que es refereix als jocs d’atzar. Buffon es va adonar que «l’anàlisi va ser l’única eina utilitzada fins aleshores en la ciència de les probabilitats, com si la geometria no fóra apropiada per a tal fi quan, en realitat, nomes cal parar un poc d’atenció per percebre que l’avantatge de l’anàlisi sobre la geometria és només accidental i que l’atzar és tan propi de la geometria com de l’anàlisi». I afegeix: «per donar a la geometria la posició dels drets que té sobre la ciència de l’aleatori, només caldrà inventar jocs que es basen en l’extensió i les relacions d’aquesta». A continuació, esmenta el joc anomenat franc-carreau; és a dir, sobre un terra quadriculat es llança a l’atzar una moneda i es demana la probabilitat que caiga dins d’un dels quadrats, sense tallar cap de les línies de separació. El de l’agulla de Buffon és un problema en la línia de l’anterior, plantejat per Buffon el 1733 i reproduït per ell mateix, ja resolt, utilitzant mètodes ad hoc, el 1777. Es tracta de llançar una agulla de longitud l sobre un terra on s’han dibuixat rectes paral·leles, a distància d entre dues consecutives (d > l). Buffon va demostrar, d’una manera intuïtiva, que la probabilitat que l’agulla talle una de les línies és p = 2l / d π. Arran del problema de l’agulla de Buffon es va desenvolupar tota una teoria matemàtica i algunes implicacions directes d’aquest problema, com veurem més endavant, encara són utilitzades en estereologia pràctica. Del problema de Buffon al naixement d’una teoria matemàtica Una primera observació del problema de l’agulla de Buffon posa de manifest que, llançada l’agulla, algunes posicions d’aquesta faran que talle alguna de les línies i altres posicions no; però, com podem determinar i mesurar aquestes posicions? Aquesta és una de les qüestions que van motivar el naixement de la geometria integral. La solució que es va adoptar per resoldre-la va ser dotar l’agulla (un segment) d’un element de mesura invariant respecte al grup de moviments (és a dir, respecte a translacions i rotacions). D’aquesta manera, cada problema semblant al de l’agulla de Buffon té una solució única que no depèn de l’elecció de paràmetres per fixar el segment, ni dels eixos de coordenades. Així doncs, fou el matemàtic anglès Crofton el primer a definir el que s’ha d’entendre per rectes a l’atzar i per mesures de conjunts d’aquestes; i a donar, d’aquesta manera, una solució formal al problema de Buffon. El nom de «geometria integral» va ser introduït el 1936 per Wilhelm Blaschke en una sèrie de treballs basats, fonamentalment, en l’obtenció de resultats geomètrics en el camp dels cossos convexos, a partir d’algunes idees sobre probabilitat geomètrica. Des de la introducció de la geometria integral fins que va anar adquirint entitat de teoria matemàtica foren molts els conceptes que es van adaptar d’altres parts de la matemàtica, sobretot de la geometria diferencial i, en particular, de la geometria de Riemann, i que van donar suport al desenvolupament d’aquesta proporcionant-li el llenguatge i l’estructura necessaris. Entre els matemàtics que van fomentar el desenvolupament de la geometria integral cal destacar Chern, Santaló i Stokes, entre d’altres. Hem vist que la necessitat de mesurar posicions de segments en el pla va significar l’origen de la geometria integral. Però un altre escull important en el problema de Buffon, que va ajudar a desenvolupar aquesta teoria, era estendre al context geomètric el popular concepte de probabilitat com a «nombre de casos favorables dividit pel nombre de casos possibles», senzill, o almenys natural quan es tracta d’experiments els casos possibles dels quals són finits, com ara els jocs de daus o cartes, però no tan natural en el cas de l’agulla de Buffon. El concepte de «nombre de casos» se substitueix pel de «mesura invariant de posicions d’un objecte geomètric» (agulla) que satisfà una condició donada (que l’agulla talle una recta). Aquesta mesura és una integral respecte a l’element de mesura invariant. Així doncs, tret de comptades excepcions, la probabilitat geomètrica i la geometria integral es desenvolupen obeint a un interès purament matemàtic, al marge d’aplicacions concretes. Ara bé, si a un li diuen que en un mil·límetre cúbic de múscul hi ha al voltant d’un metre i mig de capil·lars sanguinis i que aquesta estimació es realitza a través de la visió d’imatges planes mitjançant microscòpia; utilitzant conceptes derivats de la geometria integral; és a dir, utilitzant mesures de plans en l’espai per estimar longituds de corbes; l’assumpte també promet ser interessant. I és que l’estereologia, definida com «la ciència de la interpretació tridimensional d’imatges planes», proporciona els mètodes més eficients per estimar, sense esbiaixaments, quantitats geomètriques com volum, àrea de superfície, longitud, nombre o connectivitat, a partir de seccions o projeccions de l’espai de referència. |
© Musée Buffon, Montbard «Influït per la seua època, Buffon va considerar les passions com intrínseques de l’ésser humà i va dedicar especial atenció als jocs d’atzar»
«Buffon es va adonar que l’anàlisi havia estat l’única ciència utilitzada fins aleshores
«Un altre escull important en el problema de Buffon era estendre al context geomètric el popular concepte de probabilitat com a “nombre de casos favorables dividit pel nombre de casos possibles”»
|
|
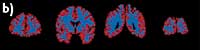
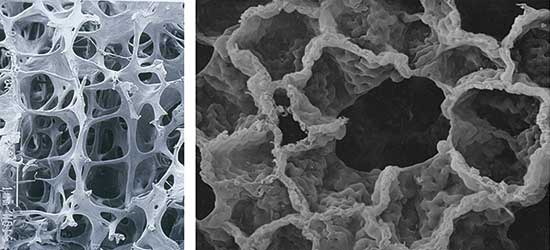 Font: L. Mosekilde, Universitat d’Aarhus / Font: Gehr, P. et al, 1981. Respiration Physiology, 44:61-86. Si en lloc d’estimar el volum d’un sòlid es pretenen estimar altres quantitats geomètriques com la connectivitat, que té relació amb malalties com l’osteoporosi (a l’esquerra, os afectat per la malaltia) o l’àrea d’una superfície, com pot ser la superfície alveolar (figura de la dreta), aleshores tant l’obtenció de l’estimador, a partir d’imatges planes, com l’estudi de l’error comès es compliquen considerablement. |
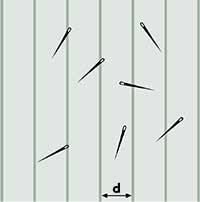
«El problema de Buffon consisteix a llançar una agulla sobre una superfície amb rectes paral·leles. Quina és la probabilitat que l’agulla talle una d’aquestes rectes?» |
|
|
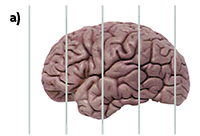
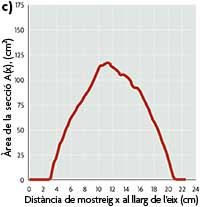
Des del 1961, quan es va fundar la Societat Internacional d’Estereologia, aquest àmbit d’investigació s’ha assentat sòlidament en la teoria del mostreig geomètric i la geometria integral, sempre inspirat en les aplicacions. Una llista parcial de disciplines on s’utilitza l’estereologia inclou l’anatomia, la fisiologia, les neurociències, la radiologia, la mineralúrgia; com també la botànica (com si el comte de Buffon ja fóra conscient, en el seu moment, d’aquesta connexió). A més d’aquestes disciplines, que requereixen de l’estereologia, l’anàlisi d’imatge n’és una àrea subsidiària, adreçada a l’observació i mesura automàtiques d’imatges de seccions. L’estereologia s’encarrega de fer que els mostreigs siguen adequats. També cal comentar que, recentment, s’ha començat a relacionar amb èxit l’estereologia amb la tomografia computeritzada; així doncs, les propietats quantitatives d’objectes geomètrics que persegueix l’estereologia comencen a relacionar-se amb les propietats qualitatives (reconstrucció tridimensional, etc.), que s’obtenen mitjançant la tomografia. Però, què és l’estereologia? Potser la manera més senzilla d’explicar què és l’estereología siga cenyir-se a un exemple d’estimador senzill i intuïtiu. L’estimador més clàssic, sens dubte, és l’estimador de Cavalieri, que deu el seu nom al matemàtic italià Bonaventura Cavalieri (1598–1647), que va ser deixeble de Galileu. El paràmetre que es desitja estimar és el volum d’un objecte fitat. I per a fer-ho els passos seguits en el mostreig i estimació són els següents: fixem un eix i intersequem l’objecte mitjançant un conjunt sistemàtic de plans paral·lels perpendiculars a l’eix fixat. La distància entre dos d’aquests plans consecutius és una quantitat fixa T. L’abscissa z d’un d’aquests plans (punt intersecció entre el pla i l’eix) es tria de manera aleatòria i uniforme en l’interval (0, T). D’aquesta manera, l’estimador del volum de l’objecte és igual a la suma de les àrees d’intersecció entre l’objecte i els plans paral·lels, multiplicada per la distància T entre plans consecutius. Per tant, a partir de l’observació de l’àrea de les seccions planes estimem el volum de l’objecte. Aquest estimador es continua utilitzant en l’actualitat i, encara que es tracte d’un estimador senzill, l’estudi de propietats com ara l’error comès en l’estimació, que depèn de la distància T, com el mateix Santaló va posar de manifest, és una tasca àrdua i difícil que encara ara és objecte de recerca en estereologia. El problema de Buffon a hores d’ara Una vegada analitzada l’aparició i l’evolució de la geometria integral i de l’estereologia, a partir del problema de Buffon, tornarem la nostra atenció sobre aquest problema per desenvolupar, com a aplicació directa d’aquest, dues qüestions curioses. La primera consisteix a mesurar el valor numèric del nombre π i la segona, a mesurar la longitud d’una corba plana mitjançant el recompte del nombre de punts d’intersecció de la corba i d’un feix de rectes paral·leles (sonda). Tornem al problema de Buffon. Sabem que l’agulla talla alguna de les rectes amb probabilitat p = 2l / d π. Suposem que llancem l’agulla N ocasions i en n d’aquestes l’agulla interseca alguna de les rectes; aleshores una estimació de la probabilitat p és p* = n / N, i, per tant, podem considerar com estimador de π, π* = 2l / d p*. L’estudi de l’error comès en aquesta estimació ha donat lloc a un nombre elevat de treballs científics en els quals es combinen desenvolupaments teòrics amb resultats experimentals. Seguint una argumentació similar a l’anterior, i partint d’una corba plana com la unió d’un conjunt de segments, resulta fàcil deduir que un estimador de la longitud de la corba és l* = d π J / 2, sent J el nombre de talls de la corba plana amb el feix de rectes paral·leles. Es demostra que aquest estimador no és esbiaixat i continua sent vàlid si se substitueix la sonda formada per rectes paral·leles per una altra sonda de forma arbitrària. Aquest estimador es continua utilitzant en tots els paquets informàtics d’estereologia pràctica, que vénen adaptats en microscòpia. Després de fer aquest breu recorregut des de la geometria integral fins l’estereologia, utilitzant com a eix el problema de l’agulla de Buffon, em ve a la memòria la resposta que va donar un especialista en preguntar-li per què s’havia dedicat a l’estereologia: «Suposo que el fet d’haver estat obsessionat, o més aviat condicionat, per certes mesures des de menut ha influït en l’elecció», va dir. En el meu cas també m’agradaria pensar que l’afició per l’estereologia ha estat influïda per una mesura mítica com són els 1.813 metres del pic de Penyagolosa. Ximo Gual Arnau. Departament de Matemàtiques, Universitat Jaume I de Castelló. |
Esquema del problema de l’agulla de Buffon, que consisteix a llançar una agulla amb una determinada longitud (l) sobre una superfície on s’han dibuixat rectes paral·leles amb un distància (d) determinada entre elles i calcular la probabilitat que l’agulla talle una d’aquestes línies. Buffon va demostrar que aquesta probabilitat és de p = 2l / d π.
«L’estereologia és definida com la ciència de la interpretació tridimensional d’imatges planes»
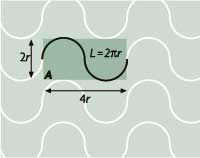
Sonda general, formada per cicloides en lloc de rectes paral·leles. El problema de l’agulla de Buffon es pot modificar seguint el mateix esquema però canviant les rectes paral·leles per altres sondes més generals com, per exemple, conjunts de cicloides sobre el pla. En el dibuix, A representa l’àrea del rectangle en verd obscur i L és la longitud de la corba que està dins d’aquest, longitud que coincideix amb la d’una circumferència de radi r. |
El problema de l’agulla de Buffon