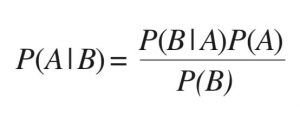La teoria que no va morir mai

La regla de Bayes, una teoria senzilla del segle XVIII per a l’avaluació del coneixement, rebé tot de crítiques durant la major part del segle XX, però va ser utilitzada pel Regne Unit i els Estats Units durant la Segona Guerra Mundial i la Guerra Freda. Palomares i València van representar papers importants en el seu desenvolupament durant aquells temps ombrívols. L’ús de la regla està molt estès avui dia en l’àmbit de la computació i en moltes aplicacions més. Per exemple, Bayes s’ha convertit en la clau política per a la presa de decisions basades en dades. La revolució bayesiana ha esdevingut un canvi de paradigma modern per a una era eminentment pragmàtica.

Paraules clau: regla de Bayes, Fisher, freqüentistes, Laplace.

Recentment, una simple teoria matemàtica descoberta per dos clergues britànics (Bayes, 1763) en el segle XVIII ha pres per assalt el món modern, dominat pels ordinadors. De fet, és una part tan generalitzada de les nostres vides informatitzades que s’ha convertit en chic –fins i tot en políticament correcta– en alguns sectors importants dels Estats Units.

No obstant això, durant la major part del segle XX va ser tan controvertida que molta de la gent que la utilitzava no gosava ni tan sols a mencionar-la. Durant el període més tempestuós de la història de la regla de Bayes, dos llocs d’Espanya –Palomares i València– van fer un paper vital per a mantenir viva la teoria.

De simple, la teoria resulta gairebé ridícula. Ajuda la gent a avaluar les seues idees inicials, a actualitzar-les i modificar-les amb nova informació i a prendre millors decisions. En resum, la regla de Bayes és molt breu i senzilla: Creences inicials + dades objectives recents = Una nova creença millorada.

Com l’il·lustre economista britànic John Maynard Keynes va dir amb sorna, «Quan els fets canvien, canvie d’opinió. Què fa vostè, senyor?»

Durant el segle XVIII, dos clergues i matemàtics aficionats, l’anglès Thomas Bayes i el seu amic gal·lès Richard Price, van descobrir i van publicar el teorema, i el matemàtic francès Pierre-Simon Laplace el va desenvolupar en la forma en què s’usa avui dia. Ara podríem dir-ne la teoria Bayes-Price-Laplace, o BPL per a abreviar.

La teoria és molt consistent. En la pràctica, la regla de Bayes requereix múltiples càlculs, i potents ordinadors que reintegren milions de vegades la probabilitat d’una creença inicial cada vegada que arriba informació nova. La regla de Bayes no genera una resposta absolutament certa, exacta. En canvi, utilitza la probabilitat per a moure’s pas a pas cap a la conclusió més probable. No obstant això, gràcies a Bayes, podem filtrar correu brossa, avaluar riscos mèdics o d’un altre tipus, cercar les pàgines que ens interessen en Internet i descobrir el que potser ens interessaria comprar, aprofitant l’historial de les cerques que hem fet en el passat. L’exèrcit fa servir aquesta regla per a millorar les imatges generades durant el vol dels drones, i els doctors, per a millorar les nostres ressonàncies magnètiques i estudis PET. S’utilitza en Wall Street, en astronomia i en física, en traducció automàtica de llengües estrangeres, genètica i bioinformàtica. La llista no acaba.

«Una simple teoria matemàtica descoberta per dos clergues britànics en el segle XVIII ha pres per assalt el món modern, dominat pels ordinadors»

Prova A del poder actual de la regla de Bayes: trobar objectes perduts al mar. Durant la Guerra Freda, la Força Aèria dels Estats Units va perdre una bomba d’hidrogen a la costa de Palomares, i la Marina dels Estats Units va començar a desplegar la teoria bayesiana en secret per a trobar objectes davall l’aigua. El 2009, el vol 447 d’Air France va desaparèixer en l’oceà Atlàntic Sud amb 228 persones a bord. La Marina dels Estats Units havia desenvolupat la teoria de cerca bayesiana prou per acabar amb dos anys de cerca infructuosa de l’AF447 en una setmana de cerca submarina. Els experts en la recerca bayesiana esperen que la teoria també ajude a trobar el vol 370 de Malaysian Airlines.

Per a la prova B del poder de Bayes tenim el cotxe sense conductor de Google, que comença a rodar amb la informació de mapes de ruta i de les condicions de la carretera. A mesura que l’automòbil es mou en entorns de trànsit, els sensors que porta a sobre arrepleguen noves dades de trànsit per actualitzar la informació inicial i calcular quina és probablement la conducció més segura en aquell moment.

La prova C del poder actual de Bayes té a veure amb els filtres de correu brossa. Molta gent, inclosa jo mateixa, recorda començar el treball de cada dia esquivant anuncis de Viagra. Per sort, això va canviar quan l’any 2000 se li va concedir a Microsoft una patent per a filtres bayesians de correu brossa.

Benjamin West. Richard Price, 1784. Oli sobre llenç, 87,5 × 185 cm. Price va acabar convençut que el teorema ajudaria a provar l’existència de Déu com a causa. Després de dos anys editant el teorema de Bayes, el va publicar en una revista anglesa. / Llyfrgell Genedlaethol Cymru, The National Library of Wales

La Il·lustració

Però per a entendre per què una teoria tan útil havia causat tant d’enrenou durant la major part del segle XX, hem de remuntar-nos al començament, als temps dels reverends Thomas Bayes i Richard Price, durant els anys quaranta del segle XVIII. S’havia obert una dura polèmica entorn de la improbabilitat dels miracles cristians. La qüestió era si existien proves en el món natural que ens ajudaren a aconseguir conclusions racionals sobre Déu creador, allò que en el segle XVIII es coneixia com la causa o la primera causa.

No sabem si Bayes intentava demostrar l’existència de Déu com a causa. Però sí que sabem que va tractar d’enfrontar-se matemàtica­ment al problema de causa i efecte. No obstant això, Bayes no confiava prou en el seu teorema per publicar-lo. El va arxivar en un quadern i no es va descubrir fins que va morir deu o quinze anys després. En el seu testament, li va deixar a Price 100 lliures i una petició: que per favor fera una ullada als seus textos no publicats.

Revisant-los, Price va acabar convençut que el teorema ajudaria a provar l’existència de Déu com a causa. Després de dos anys editant el teorema de Bayes, el va publicar en una revista anglesa que, per desgràcia, llegien molt pocs matemàtics.

Uns anys més tard, el 1774, un gran matemàtic francès, Pierre Simon Laplace, va descobrir la regla independentment de Bayes i Price. Laplace la va anomenar probabilitat de causes. A diferència de Bayes i Price, Laplace era la quinta essència del científic professional. Va matematitzar tota ciència coneguda en la seua època i va passar quaranta anys desenvolupant ocasionalment el que coneixem com la regla de Bayes (Laplace, 1812). De fet, fins fa uns cinquanta anys, la regla de Bayes es considerava part de l’obra de Laplace. Per dret, encara hauríem de conèixer-la com la regla de Laplace.

Després de la mort de Laplace el 1827, una actitud molt diferent sobre l’avaluació de l’evidència científica es va apoderar del món de l’estadística. En el transcurs dels segles XVIII i XIX a Occident, els científics, governants, empresaris i clubs d’aficionats van acumular una gran quantitat de dades precises i fiables. Algunes d’aquelles famoses col·leccions de dades mesuraven la grandària del tòrax dels soldats escocesos, el nombre d’oficials prussians que morien a causa de la guitza d’un cavall i la incidència del còlera.

La reacció anti-Bayes

Amb una gran quantitat de nombres precisos i fiables al seu abast, els estadístics van rebutjar la regla de Bayes; s’estimaven més jutjar la probabilitat d’un esdeveniment d’acord amb la freqüència amb què es produïa. Amb el temps, se’ls va conèixer com freqüentistes. Fins fa uns anys, havien estat el gran adversari de la regla de Bayes.

Per als freqüentistes, la ciència moderna requeria tant objectivitat com respostes precises. Mesurar la creença inicial i subjectiva d’algú i computar les probabilitats i aproximacions semblava «subjectivitat sense control», «una aberració de l’intel·lecte» i «ignorància […] disfressada de ciència». Cap a 1920 la majoria de científics pensaven que Bayes era «una galtada d’astrologia, d’alquímia». I un estadístic important va dir que la fórmula de Bayes s’usava «amb un bufit de resignació, sabent que és l’únic instrument que tenim al nostre abast en algunes circumstàncies».

«Bayes no confiava prou en el seu teorema per publicar-lo. El va arxivar en un quadern fins que va morir anys després»

És sorprenent que en tot aquest temps –mentre teòrics i filòsofs denunciaven l’aberració subjectivista que segons ells era la regla de Bayes– la gent que havia d’enfrontar-se a les urgències de la vida real i prendre decisions vitals basant-se en informació incompleta continua­ven utilitzant la regla de Bayes. Segons la seua opinió, la regla els ajudava a apanyar-se-les amb el que tenien.

Així, per exemple, la regla de Bayes va ajudar a alliberar Dreyfus d’una presó francesa on l’havien tancat per traïció en la dècada de 1890. Els oficials d’artilleria a França, Rússia i els EUA la van utilitzar per apuntar i posar a prova les seues municions i canons durant les dues guerres mundials. Els executius de les companyies d’assegurances i telefòniques també utilitzaven la regla de Bayes als Estats Units durant la Primera Guerra Mundial.

Ara bé, tota bona història necessita un dolent, i el dolent de la nostra és un gran estadístic, Ronald Aylmer Fisher, de la Universitat de Cambridge. Durant els anys vint i trenta del segle XX, la mecànica quàntica va desfermar una reacció cultural contra la probabilitat i la incertesa, i els teòrics estadístics com Fisher van canviar la seua actitud respecte a Bayes, de tèbia tolerància a absoluta hostilitat.

Jean-Baptiste Guérin Paulin. Pierre-Simon marquis de Laplace (1745-1827), 1838. Oli sobre llenç, 113 × 146 cm. El 1774, el matemàtic francès Pierre Simon Laplace va descobrir la regla independentment de Bayes i Price i la va anomenar probabilitat de causes. / Grand Palais (Château de Versailles)

Els atacs de Fisher van ser especialment importants perquè era un gegant d’una estadística que anava encara en bolquers (Fisher, 1925). També tenia un temperament explosiu, que ell mateix reconeixia que li «amargava l’existència». Un col·lega va titllar Fisher d’«home polèmic i controvertit. La seua vida va ser una interminable cadena de batusses científiques –que de vegades arribaven fins i tot a simultaniejar-se–, ja fora en les reunions entre professionals o en els articles propis de l’ofici». Fins i tot interpretava qüestions científiques com a atacs personals. I odiava la regla de Bayes.

Fisher no necessitava Bayes. Bayes és especialment útil quan les dades són escasses i incertes, i Fisher tenia dades precises sobre quant de fertilitzant s’havia utilitzat en uns camps determinats. Va omplir sa casa de gats, gossos i milers de ratolins per a experiments de cria i, com a bon apassionat de l’eugenèsia i la genètica, va documentar el pedigrí de cada animal durant generacions. Els seus experiments eren repetibles i van produir respostes precises. Va qualificar la regla de Bayes d’«única equivocació (tal vegada l’única equivocació amb què el món de la matemàtica es troba implicat mai a fons) […] fonamentada en un error i [la regla] ha de ser rebutjada completament». Després que un altre científic i estadístic de Cambridge, Harold Jeffreys, usara la regla de Bayes per trobar terratrèmols a partir dels tsunamis que van provocar, Fisher va dir que en el seu llibre sobre probabilitat (Jeffreys, 1931) havia comès «en la primera pàgina del seu escrit un error lògic que invalida les 395 fórmules de la resta del llibre». L’error, per descomptat, és que aprofitava la regla de Bayes (Aldrich, 2004, 2008).

La Segona Guerra Mundial

Per tant, al començament de la Segona Guerra Mundial el 1939, Bayes era gairebé un tabú entre els estadístics més sofisticats. Afortunadament per a la Gran Bretanya i els Estats Units, Alan Turing no era un expert en estadística. Era matemàtic. Com que necessitava prendre decisions urgents basades en proves exigües, Turing va usar la regla de Bayes àmpliament, primer, per desxifrar les ordres per als submarins en l’Atlàntic Nord amagades en el codi Enigma dels alemanys; i segon, per construir les computadores Colossus, dissenyades per desxifrar altres codis alemanys durant la guerra.

«Gràcies a Bayes podem filtrar correu brossa, avaluar riscos mèdics, buscar les pàgines que ens interessen en Internet i descobrir el que potser ens interessaria comprar»

Després de la Pax Europaea, però, el govern britànic va classificar com a secret d’estat tot allò que mostrara que les matemàtiques, l’estadística, les descodificacions, les computadores i Alan Turing havien ajudat a guanyar la guerra. El decret potser va impedir que el Regne Unit es convertira en el líder de la revolució informàtica del segle XX. Per descomptat va impedir que matemàtics i estadístics es convertiren en herois de guerra.

Com que els seus èxits bèl·lics van quedar classificats, la regla de Bayes va arribar al final de la Segona Guerra Mundial despertant més suspicàcies que abans. Després que Jack Good, l’assistent estadístic de Turing durant la guerra, exposara els detalls del mètode davant dels membres de la Real Societat Estadística britànica, les primeres paraules del següent orador van ser: «Després d’aquestes estupideses…» Els professors de l’Escola d’Estudis Empresarials de Harvard deien que els seus col·legues bayesians eren uns «socialistes que s’autodenominaven científics». Quan Hans Buehlmann, futur president de l’Escola Politècnica Federal de Zuric (ETH), va visitar el departament d’estadística de Berkeley, profundament freqüentista, va afirmar que «era quasi perillós exposar-hi el punt de vista bayesià». Així, doncs, va utilitzar el mètode de Bayes, però va haver d’inventar una terminologia diferent i neutral que, segons la seua opinió, protegia l’Europa continental de gran part del menyspreu angloamericà.

Durant la Guerra Freda, la Força Aèria dels Estats Units va perdre una bomba d’hidrogen a la costa de Palomares, i la Marina dels Estats Units va començar a desenvolupar la teoria bayesiana en secret per trobar objectes davall l’aigua. En la imatge, el casquet de dues bombes nuclears B28 de l’incident de Palomares, exposades al Museu Nacional de la Ciència i la Història Nuclear, en Albuquerque, Nou Mèxic. / Plumbob78

Irònicament, quan Bayes es va convertir en un tema tabú, l’exèrcit nord-americà va continuar utilitzant-lo en secret. Per exemple, un estudi classificat de la Corporació RAND a Califòrnia va usar la regla de Bayes per avisar la Força Aèria dels Estats Units que continuar pilotant avions armats amb bombes d’hidrogen pel món podia causar més accidents com el de Palomares. L’administració Kennedy finalment va afegir-hi dispositius de seguretat. La Marina dels Estats Units la va utilitzar per trobar submarins soviètics al Mediterrani. El 1973, el primer estudi de seguretat de la indústria d’energia nuclear dels Estats Units es va basar en mètodes bayesians i va predir el que passaria durant l’accident de 1979 a Three Mile Island, Pennsylvania.

Ressorgiment i prova del seu valor

Sense conèixer els èxits de la regla de Bayes, un petit grup d’uns cent o més creients van batallar perquè s’acceptara durant la Guerra Freda. Molts bayesians d’aquella generació recorden el moment exacte en què la lògica general de Bayes els va trasbalsar de colp com una epifania. Per a ells, la regla de Bayes tenia allò que Einstein va anomenar «el sentiment religiós del cosmos».

La batalla entre estadístics bayesians i antibayesians es va tornar tan corrosiva i personal que, en una festa a mitjan anys seixanta a la qual un bayesià nord-americà va portar el seu fill de nou anys, un invitat va dir al xic que «son pare era un home profundament enganyat».

Esquerra: L’exèrcit fa servir la teoria de Bayes per a millorar les imatges generades durant el vol dels drones / Don McCullough. Dreta: El cotxe sense conductor de Google comença a rodar amb la informació de mapes de ruta i de les condicions de la carretera. A mesura que l’automòbil es mou en entorns de trànsit, els sensors que hi ha sobre el vehicle arrepleguen noves dades de trànsit per a actualitzar la informació inicial i calcular quina és probablement la conducció més segura en aquell moment. / Steve Jurvetson

Durant aquest període angoixós, José M. Bernardo, un professor d’estadística de la Universitat de València, va utilitzar mètodes bayesians radicalment nous en aquell moment per a realitzar anàlisis polítiques. Va realitzar una anàlisi bayesiana d’enquestes polítiques per al Partit Socialista el 1982, durant les eleccions que li donarien el poder a Felipe González. La regla de Bayes és útil per a actualitzar hipòtesis amb dades molt diverses, incloent-hi la probabilitat d’actituds i tendències de vot. Més tard, Bernardo es va convertir en assessor científic del govern durant la presidència de González i va dur a terme altres aplicacions bayesianes. Mentrestant, Bernardo també va representar un paper important per a la camaraderia bayesiana. Va convèncer el primer govern democràtic (centrista) després de la dictadura feixista que finançar un congrés internacional per a estadístics bayesians el 1979 ajudaria a publicitar l’emergent estat democràtic espanyol. L’esforç va tenir tant d’èxit que el govern valencià va finançar una segona i una tercera conferència. Després d’això, ja no en calien, de subvencions, ja que es considerava un privilegi ser invitat i els estadístics podien obtenir diners fàcilment de les seues institu­cions per al viatge. Altres fons van proporcionar beques a nous doctorats. Les reunions, que se celebraven cada quatre anys, eren vitals perquè els bayesians desenvoluparen un sentiment de solidaritat, per revifar els esperits i discutir els últims mètodes i teories. Amb els anys, les conferències van créixer i van passar de prop de cent assistents a tants que el congrés va haver de traslladar-se a instal·lacions cada vegada més grans. Ara una organització internacional de bayesians (ISBA) continua organitzant el congrés cada dos anys: a Kyoto, Japó, el 2012 i a Cancun, Mèxic, el 2014.

Durant la dècada de 1990 el panorama va canviar radicalment per a la regla de Bayes. Potents ordinadors personals, nous mètodes computacionals i el programari lliure finalment van permetre als bayesians calcular problemes reals amb facilitat. Estudiosos de la informàtica, la física i la intel·ligència artificial van arribar en massa revitalitzant, ampliant, despolititzant i secularitzant el món de l’estadística. Després de 250 anys de vaivens, la teoria es va adoptar d’un dia per l’altre.

Alan Turing va usar la regla de Bayes àmpliament per a, primer, desxifrar les ordres per als submarins en l’Atlàntic Nord amagades en el codi Enigma dels alemanys; i segon, per a construir les computadores Colossus, dissenyades per a desxifrar altres codis alemanys durant la guerra. En la imatge, una estàtua del matemàtic en el Bletchley Park Museum. / Duane Wessels (Bletchley Park Museum)

Durant els últims anys, Bayes s’ha convertit en una figura que molts nord-americans moderns pensen que haurien de conèixer. Per exemple, quan Alan B. Krueger es va convertir en membre del consell d’assessors econòmics del president Obama, va fer una menció completament gratuïta del meu llibre sobre Bayes ­(McGrayne, 2013) en el New York Times: «Recentment he acabat de llegir el llibre de McGrayne […] la regla de Bayes és una teoria estadística amb una història llarga i interessant. És important en la presa de decisions –com d’estricte que cal ser a l’hora d’aferrar-se a idees pròpies i com cal anar actualitzant aquestes idees d’acord amb la nova informació que es va rebent. Nosaltres […] [i recordem que és conseller d’Obama] usem la regla de Bayes intuïtivament cada dia.»

Així doncs, de sobte en aquesta era dogmàtica, quan molts líders estan orgullosos de prendre decisions basades en la doctrina que van rebre de nens, Bayes s’ha convertit en la clau política per a una cosa diferent: la presa de decisions basades en dades. Després d’un notable desenvolupament, l’estadística bayesiana –que va ser camp d’estudi de clergues i de cent creients assetjats durant la Guerra Freda– és ara part del vocabulari de la Casa Blanca.

La revolució bayesiana ha resultat ser un canvi de paradigma modern per a una era eminentment pragmàtica. Va succeir del dia a la nit. No perquè la gent canviara d’opinió sobre la regla de Bayes com a filosofia científica, sinó perquè de sobte la regla funcionava.