Quan la tecnologia va més ràpid que la comprensió

L’aprenentatge profund és un tema indiscutiblement candent, no sols entre acadèmics i indústria, sinó també en la societat i en els mitjans de comunicació. Les raons d’aquesta popularitat creixent són múltiples: una disponibilitat sense precedents de dades i potència de càlcul, l’aparició d’algunes metodologies innovadores, trucs tècnics menors però significatius, etc. No obstant això, és curiós que l’èxit actual i la pràctica de l’aprenentatge profund pareixen no estar correlacionats amb la comprensió més teòrica i formal d’aquest camp. A causa d’això, l’avantguarda tecnològica de l’aprenentatge profund presenta una sèrie de propietats o situacions poc intuïtives. En aquest text es ressalten algunes d’aquestes propietats poc intuïtives, i es tracta de mostrar treballs recents rellevants i de posar de relleu la necessitat de saber més sobre la matèria, ja siga mitjançant mètodes empírics o formals.

Paraules clau: aprenentatge profund, aprenentatge automàtic, xarxes neuronals, propietats poc intuïtives.

Introducció

En els últims anys, les xarxes neuronals han ressorgit de les seues cendres i han produït resultats impressionants en tasques per a les quals el rendiment dels mètodes tradicionals era sistemàticament inferior (LeCun, Bengio i Hinton, 2015). N’hi ha moltes, de raons d’aquest èxit, i continuen sent tema de debat. Per descomptat, la contribució de certes dades i components tecnològics, com la disponibilitat de volums de dades sense precedents i l’accés generalitzat a una major potència de càlcul, ha estat decisiva. No obstant això, a més d’aquests components més pràctics, podríem dir amb seguretat que un dels principals facilitadors de l’èxit actual de les xarxes neuronals ha estat la introducció d’alguns «trucs de l’ofici» menors però significatius. Alguns exemples van ser la inicialització dels pesos de les neurones mitjançant entrenament previ no supervisat, la substitució de les activacions sigmoides per unitats lineals rectificades per a alleujar el problema de la desaparició dels gradients, o l’ús sistemàtic i ampli d’arquitectures convolucionals per a abordar les traduccions reduint el nombre de pesos entrenables.

«En els últims anys, Les xarxes neuronals han ressorgit de les seues cendres i han produït resultats impressionants»

Curiosament, la majoria d’aquests trucs útils no sorgeixen d’una teoria unificada de xarxes neuronals ni de desenvolupaments matemàtics rigorosos. Al contrari, sorgeixen de la intuïció, de la investigació empírica i, en última instància, de l’assaig i error (o de cerques per força bruta). En aquest sentit, la investigació en aprenentatge profund sembla que segueix el paradigma de Wolfram d’«un nou tipus de ciència», que indica que «només podem acostar-nos al disseny òptim dels sistemes [d’aprenentatge profund] mitjançant una cerca combinatòria entre la ingent quantitat de configuracions possibles [de la xarxa]» (Wolfram, 2002). De fet, alguns investigadors han abraçat aquest mantra directament i han començat a buscar guiats parcialment per metodologies automàtiques o estructurades. Per exemple, Zoph i Le (2016) descobreixen noves configuracions de xarxa utilitzant estratègies evolutives.

Però l’avenç empíric de la disciplina no hauria d’evitar el desenvolupament de teories més formals (o prototeories) que ens permeten entendre què està ocorrent i, amb el temps, proporcionen una comprensió més holística d’aquest camp d’investigació. En particular, aquesta comprensió podria arribar gràcies a una sèrie de qüestions obertes o propietats poc intuïtives de les xarxes neuronals que desconcerten la comunitat d’investigadors (Larochelle, 2017). En la resta de l’article presentaré i intentaré explicar breument algunes d’aquestes propietats.

Les xarxes neuronals poden cometre errors absurds

Ara és ben sabut que les xarxes neuronals poden generar resultats completament inesperats a partir d’entrades amb canvis perceptivament irrellevants, coneguts habitualment com a exemples adversaris. Els humans també es poden veure desconcertats per «exemples adversaris»: tots hem vist imatges que identificàvem com una cosa (o com a part d’una cosa) i que després hem descobert que eren una altra distinta. No obstant això, la qüestió ací és que els exemples adversaris humans no es corresponen amb els de les xarxes neuronals perquè aquests últims poden ser perceptivament iguals. Szegedy et al. (2014) van mostrar que una xarxa pot classificar erròniament una imatge només aplicant-li «una certa pertorbació a penes perceptible». No sols això, també van descobrir que la mateixa pertorbació d’aquella imatge en particular provocava l’error de classificació fins i tot quan la imatge no estava en el grup d’entrenament; és a dir, quan s’havia entrenat a la xarxa amb un subconjunt d’imatges diferent. De la mateixa manera, Nguyen, Yosinski i Clune (2015) van mostrar que és possible produir imatges artificials que són completament irrecognoscibles per als humans però que, no obstant això, les xarxes neuronals profundes poden relacionar amb objectes reals amb una confiança del 99,99 %.

El problema dels exemples adversaris és interessant perquè aquests contradiuen una de les qualitats més conegudes i extensament demostrades de les xarxes neuronals: la gran capacitat de generalització que mostren (o, en altres paraules, el rendiment excep­cional amb dades noves). Cada vegada sabem més sobre potencials atacs adversaris (Papernot et al., 2017), i amb aquest coneixement apareixen noves tècniques per a enfrontar-se al problema. Han aparegut teories incipients, i el treball recent suggereix que els exemples adversaris estan directament relacionats amb el rendiment model (Gilmer et al., 2018). No obstant això, fins ara continuem sense aconseguir una comprensió general del fenomen.

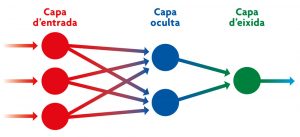
Les xarxes neuronals artificials prenen com a model el sistema neuronal d’un cervell biològic. Cada node de l’esquema representa una d’aquestes neurones situades a distints nivells (capa d’entrada, oculta i d’eixida) que processen les dades amb què se les «entrena» en el procés d’aprenentatge profund. / Adaptat de Wikipedia

L’espai de solucions és un misteri

Com passa amb molts algoritmes d’aprenentatge auto­màtic, l’entrenament de xarxes neuronals opera trobant la combinació de nombres –anomenada paràmetres de la xarxa o pesos– que ofereix el major rendiment o, millor dit, la menor pèrdua d’algunes dades. Si tinguérem un únic pes, entrenar la xarxa consistiria a trobar el valor del dit pes que ofereix la menor pèrdua d’informació. Hi ha metodologies molt conegudes que ofereixen garanties teòriques per a trobar aquell mínim en casos que inclouen una petita quantitat de paràmetres. No obstant això, les xarxes neuronals profundes solen tenir diversos milions de paràmetres, i cal combinar-los de manera apropiada per a minimitzar una determinada pèrdua. El nombre de paràmetres no seria per si mateix un problema greu si la pèrdua fora convexa; és a dir, si tinguera un únic mínim i, grosso modo, tots els camins descendents arribaren al dit mínim. Però això no és així. Les pèrdues de les xarxes profundes actuals no són convexes i tenen múltiples mínims locals.

En aquest escenari, no hi ha moltes garanties teòriques de la utilitat de la majoria de metodologies conegudes per a trobar un bon mínim (idealment el menor de tots els mínims). En general, els perfils de pèrdua induïts per les xarxes profundes són completament desconeguts, i s’ha explorat només una fracció minúscula de l’espai de solucions. A més de múltiples mínims locals, se suposa que els perfils de pèrdua inclouen punts d’enselladura (Dauphin et al., 2014) i altres obstacles que teòricament entrebanquen la «navegació» dels algoritmes actuals de cerca de mínims. No obstant això, algoritmes molt senzills de cerca de mínims extremadament bàsics aconsegueixen bones solucions; prou bones per a abordar diferents problemes d’avantguarda ben definits, i per a enfrontar-se a tasques d’aprenentatge automàtic noves i impensables fins llavors. Per què ocorre això?

«És interessant que el camp de l’aprenentatge profund puga presentar tants avenços i, al mateix temps, tantes situacions desconcertants»

Una hipòtesi comuna és que la gran majoria dels mínims locals tenen pèrdues semblants; és a dir, tots ells impliquen solucions igualment bones (Kawaguchi, 2016). Una altra hipòtesi és que, utilitzant els mètodes actuals de cerca de mínims, no es detecten els punts d’enselladura i altres obstacles (Goodfellow, Vinyals i Saxe, 2015). També és molt possible que algunes arquitectures o qüestions prèvies del disseny introduïsquen la convexitat (Li, Xu, Taylor i Goldstein, 2017). Tot això podria explicar per què funcionen realment les inicialitzacions de pes aleatòries, així com els algoritmes de cerca de mínims més simples. De fet, aquests algoritmes semblen funcionar millor quan estan mal condicionats, o quan s’introdueix soroll en el procés.

Les xarxes neuronals poden memoritzar amb facilitat

Fins i tot una xarxa neuronal no molt profunda és part del que es coneix com a algoritmes universals d’aproximació de funcions (Cybenko, 1989). En poques paraules, això significa que les xarxes neuronals són prou potents per a representar qualsevol conjunt de dades. La investigació recent mostra de manera empírica que les xarxes de grandària finita poden modelar qualsevol conjunt finit de dades, fins i tot si està compost de dades mesclades, dades aleatòries o etiquetes aleatòries (Zhang, Bengio, Hardt, Recht i Vinyals, 2017). La implicació d’això és que les xarxes neuronals poden recordar les etiquetes de qualsevol dada de l’entrenament, sense importar la naturalesa d’aquest. I recordar les dades de l’entrenament implica funcionar amb un cent per cent de precisió amb aquestes dades.

El que no és tan obvi és que, si les dades no són completament aleatòries, les xarxes neuronals són totalment capaces d’extrapolar els seus records a casos nous i generalitzar. Que aconseguisquen això quan el nombre de paràmetres model és uns quants ordres de magnitud major que el nombre d’instàncies d’entrenament és el que sembla intrigant i encara no té una justificació formal. Contradiu la clàssica regla d’or de l’aprenentatge automàtic, que prefereix models simples (que incloguen pocs paràmetres que aprendre) per a aconseguir bons resultats en la generalització. També contradiu la idea convencional segons la qual cal utilitzar alguna forma més o menys explícita de poda de paràmetres irrellevants, un procés comunament conegut com a regularització, quan el model és molt més gran que el nombre d’instàncies d’entrenament (Zhang et al., 2017).

Les xarxes neuronals es poden comprimir

La poda de paràmetres o la regularització explícita no és necessària per a generalitzar. No obstant això, se sap que es pot reduir el nombre de paràmetres d’una xarxa neuronal entrenada i mantenir-ne el rendiment tant en dades conegudes com en dades noves (Han, Mao i Dally, 2016). Es poden fins i tot «destil·lar» conjunts de xarxes neuronals i crear una xarxa més petita sense incórrer en pèrdues notables de rendiment (Hinton, Vinyals i Dean, 2014). En alguns casos, l’extensió de la poda o la compressió és sorprenent: fins a cent vegades menor, depenent del conjunt de dades i l’arquitectura de la xarxa.

«Si les dades no són completament aleatòries, les xarxes neuronals són capaces d’extrapolar els seus records a casos nous i generalitzar»

Les conseqüències pràctiques de la possibilitat de comprimir xarxes neuronals de forma considerable són òbvies, especialment quan es necessita implantar aquestes xarxes en dispositius amb pocs recursos, com els telèfons mòbils, o sistemes amb maquinari limitat, com els automòbils. Però, a més de les consideracions pràctiques, també planteja diverses preguntes: en primer lloc, necessitem una xarxa de grans dimensions? Hi ha algun gir arquitectònic que, combinat amb els algoritmes actuals de cerca de mínims, ens permeta descobrir combinacions de paràmetres útils per a aquestes xarxes petites? O només és qüestió de descobrir nous algoritmes de cerca de mínims?

L’aprenentatge es veu influït per la inicialització i l’ordre dels exemples

Com ocorre amb l’aprenentatge humà, l’aprenentatge de les xarxes actuals depèn de l’ordre en què es presenten els exemples. Els experts saben que ordenar la mostra de diferent forma produeix rendiments diferents i, en especial, que els primers exemples influeixen més en la precisió final (Erhan et al., 2010). És més, un truc que s’ha convertit en tot un clàssic és entrenar prèviament una xarxa neuronal de manera no supervisada o transferir coneixement d’una tasca relacionada per a beneficiar-se de recursos addicionals (Yosinski, Clune, Bengio i Lipson, 2014). A més, és fàcil demostrar que, encara que les inicialitzacions aleatòries dels pesos de les xarxes convergisquen en una bona solució, canviar les distribucions de pesos inicials o els paràmetres de les distribucions pot afectar la precisió final o, en el pitjor dels casos, fer que la xarxa no aprenga res (LeCun, Bottou, Orr i Müller, 2002). Encara falta molt per aprendre sobre els esquemes d’inicialització amb base matemàtica i sobre els ordres òptims de les mostres d’entrenament. Sembla difícil trobar una teoria general. A més, com que la varietat d’arquitectures de xarxes neuronals creix contínuament, a les teories individuals amb base matemàtica se’ls fa difícil mantenir-se al dia.

Tant les xarxes neuronals artificials com la ment humana es poden veure desconcertades pels «exemples adversaris», imatges que identificàvem com una cosa (o com a part d’una cosa) i que després hem descobert que eren una altra distinta. La diferència en el cas de les xarxes artificials és que aquestes poden classificar erròniament una imatge només en aplicar-li una petita variació gairebé imperceptible. En la imatge, muntatge inspirat en el meme «Chihuahua o magdalena?» que va cobrar popularitat en 2016 com a exemple de les confusions que poden afectar les xarxes neuronals d’intel·ligència artificial. / Mètode

Les xarxes neuronals poden oblidar el que aprenen

En contrast amb els éssers humans, les xarxes neuronals obliden el que aprenen. Aquest fenomen es coneix com a interferència catastròfica o oblit catastròfic, i s’ha estudiat des de començament dels anys noranta (McCloskey i Cohen, 1989). Bàsicament, quan una xarxa neuronal que s’ha entrenat per a realitzar una tasca concreta és reutilitzada per a aprendre una nova tasca, aquesta oblida completament com realitzar la primera. Més enllà de l’objectiu relativament filosòfic d’imitar l’aprenentatge humà i la qüestió de veure si les màquines haurien o no de ser capaces de fer-ho, el problema de l’oblit catastròfic té conseqüències importants per al desenvolupament actual de sistemes que consideren un gran nombre de tasques (potencialment multimodals), i per a aquells que apunten cap a un concepte d’intel·ligència més general. De moment sembla poc realista que aquests sistemes siguen capaços d’aprendre de totes les dades rellevants possibles al mateix temps o de manera paral·lela.

Al llarg dels anys hi ha hagut diversos intents de solucionar l’oblit catastròfic. Algunes de les estratègies més comunes inclouen l’ús de records, els assajos o «sons» paral·lels, estratègies d’atenció o restringir la plasticitat de les neurones (Serrà, Surís, Miron i Karatzoglou, 2018). En un sentit més general, el problema de l’oblit catastròfic pot provenir del mateix algoritme de retropropagació, que representa l’essència de l’entrenament actual de xarxes neuronals. Potser una solució elegant del problema requerisca replantejar-se completament el paradigma actual.

«Com ocorre amb l’aprenentatge humà, l’aprenentatge de les xarxes actuals depén de l’ordre en què es presenten els exemples»

Conclusió

És interessant veure que un camp d’investigació com l’aprenentatge profund, que atrau moltíssima atenció (dels acadèmics, de la indústria o dels mitjans de comunicació), puga presentar tants avenços i, al mateix temps, tantes situacions desconcertants. Sembla que l’avantguarda tecnològica continua molt per davant de la nostra comprensió, i aquesta situació podria continuar durant anys. No obstant això, també podria ocórrer que un avenç teòric menor obligue a canviar el paradigma per un altre que a la llarga facilite una aproximació més formal i matemàtica a l’aprenentatge profund. Fins llavors, l’exploració empírica continuarà essent el camí i l’eina principal per a salvar la distància entre la pràctica i la comprensió, i ens recordarà que s’aproxima un nou tipus de ciència.