
Who says Chaos has no Laws? The authors explain the idea of deterministic chaos in simple terms. They outline the two most basic laws of chaos, parameter dependence and sensitive dependence on initial conditions, the famous butterfly effect. A list of applications in different fields is given with some reasons as to why these ideas are popular.
Si bé, com deia Galileu a Il Saggiatore, l’univers està escrit en llengua matemàtica, els científics extrauen les paraules per explicar-lo del mateix fons que la resta dels mortals. La precisió que una explicació científica requereix fa, però, que ben sovint paraules d’ús quotidià adquiresquen significats prou diferents del que tenen en el llenguatge corrent. Per poc habituat que estiga el lector a la terminologia científica pot reconèixer aquestes diferències en paraules com funció, cos, moment, espectre, imaginari, complex, treball, camp… Fins i tot imaginarà la diferent reacció de dos amics, un botànic i una matemàtica, davant una frase com “trau l’arrel de pi!”.
«El determinisme més estricte és completament compatible amb la impredictibilitat més absoluta»
Moltes vegades el significat habitual d’un terme pot servir, per analogia, per a suggerir o aclarir-ne l’accepció científica. D’altres, però, pot produir certa sorpresa, i fins i tot perplexitat, trobar en un context científic certes paraules. Possiblement aquesta siga la primera reacció en sentir expressions com “teoria del caos”, o “caos determinista”. Si aquest és el cas potser convé acudir a un diccionari per dissipar dubtes. Una bona opció és anar a l’Alcover-Moll, on llegirem: “Caos, m. 1. Estat de confusió en què estava l’univers al principi de la seva creació abans que Déu posàs en les coses l’orde actual. 2. Lloc de gran confusió.” A més a més il·lustra amb cites adients de Llull i de Verdaguer aquestes accepcions. La segona ens és ben familiar. I encara més en la versió que trobem al Fabra: “Caos, … Fig. Confusió i desordre total.”
Si amb aquest bagatge tractem ara d’imaginar què pot ser una teoria científica del caos o, per si no fos prou, del caos determinista, la perplexitat està servida. Hom té normalment la idea que les diferents ciències tracten de formular les lleis que regeixen el funcionament de l’univers com un tot i dels diferents fenòmens que hi observem. I cal reconèixer que, per les raons que siga, llei i desordre, determinisme i caos, són paraules que no ens casen bé. Per tant, què deu ser això del caos determinista?
Com totes les idees, aquesta té la seua història, una llarga i variada història que, simplificant un poc, podem començar al voltant del seixantè aniversari del rei Òscar II de Suècia i Noruega l’any 1889. Amb motiu d’aquesta celebració es va convocar un premi per al millor treball relacionat amb una sèrie de problemes matemàtics plantejats. Per atractius i intrigants que siguen els detalls d’aquesta convocatòria i la seua resolució –i ho són bastant!–, no és ara el moment de repassar-los. Per a la nostra història en tindrem prou recordant que el guanyador va ser Henri Poincaré (1854-1912), una de les figures més interessants de la ciència de les darreries del segle XIX i principis del XX.
La memòria premiada (vegeu figura 1), Sur le problème des trois corps et les équations de la Dynamique, considerava un problema astronòmic ben concret, de fàcil enunciat però diabòlicament complicat. Considere el lector que el problema de Kepler, que de segur deu recordar, es pot enunciar com el problema de dos cossos (Sol-planeta). La seua solució és coneguda pels batxillers (almenys, els plans dels anys cinquanta) i no semblaria en principi que acceptar un tercer invitat anara a complicar massa les coses. Les aparences, una vegada més, enganyen.
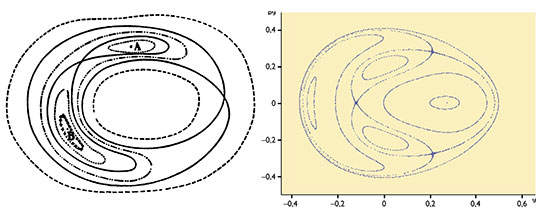
Figura 2: Les corbes de l’esquerra aparegueren en la memòria de Poincaré de 1890, i foren obtingudes amb força imaginació. Les de la dreta foren publicades el 1964 en un article dels astrònoms Hénon i Heiles, i foren construïdes a partir de càlculs amb ordinador.
I què té a veure això amb el caos? Doncs que els moviments de tres cossos controlats per la llei d’atracció universal de Newton, paradigma del determinisme laplacià i base de la concepció mecanicista del món, podien resultar terriblement complicats. I en un precís sentit tècnic Poincaré introduïa (en la versió publicada del seu treball) el concepte del que en llenguatge actual anomenem solucions caòtiques o homoclíniques, que ell anomenava doblement asimptòtiques. La figura 2, en la seua modesta aparença, és en la nostra opinió colpidora. Compara el poder d’abstracció i imaginació de Poincaré amb els resultats numèrics fets amb ordinador el 1964. Aquests corresponen a un article dels astrònoms Hénon i Heiles, que va representar un paper important en la revifalla de l’interès pel caos. Sobren comentaris.
De fet la paraula caos, en el sentit científic que ara ens interessa, sembla haver estat usada per primera vegada el 1975 en un article dels matemàtics Li i Yorke, encara que el principal resultat havia estat demostrat, fins i tot amb més generalitat, pel rus Sharkovski el 1964 en una revista ucraïnesa. Un altre dels molts exemples de l’efecte de la incomunicació científica!
Deixem, però, les qüestions tècniques i tractem d’explicar, encara que siga breument, de què va això del caos. Les teories deterministes (i la mecànica newtoniana n’és l’exemple clàssic) impliquen que, conegut perfectament l’estat d’un sistema en un instant determinat, la seua evolució posterior queda absolutament fixada. D’aquí s’infereix la possibilitat de fer prediccions. Podem immediatament objectar que mai arribarem a conèixer l’estat amb precisió absoluta i que per tant les prediccions necessàriament heretaran imprecisions inevitables. L’objecció és impecable i així s’havia acceptat tradicionalment. Però el fet no tenia més transcendència perquè hom pressuposava que els errors originats en les prediccions estaven dins dels marges d’error inherents a tota observació experimental.

Diuen que els gals només temien que el cel els caiguera al seu damunt. Potser els preocupava ja l’estabilitat del sistema solar i el caos? Aquesta és una qüestió per a historiadors. Els astrònoms diuen que podrem dormir tranquils uns quants anys. Ja deia Abraracúrcix que “això no serà per demà”…
Potser convé il·lustrar el que diem. Imaginem que representem els possibles estats d’un sistema per grans dels raïms d’una vinya. La idea clàssica és que els grans que constitueixen un carràs –o xanglot– en un instant determinat evolucionen de tal manera que després d’un cert temps els corresponents grans formaran també un altre carràs de dimensions similars a les originals. En altres paraules, no esperem mai trobar en raïms i encara menys en ceps diferents, els grans que inicialment estaven en un mateix carràs.
És clar que hi ha situacions en les quals les prediccions no es poden fer amb precisió acceptable. Podem pensar en les dificultats de les prediccions meteorològiques degudes a la gran quantitat de factors que hi poden influir. Clàssicament aquests comportaments “complicats” que limiten fortament la predictibilitat s’atribueixen únicament a la complexitat estructural del sistema considerat.
Doncs bé, la teoria del caos determinista qüestiona aquestes idees. No proposa noves lleis físiques, simplement estudia millor les equacions clàssiques i descobreix que molt sovint aquestes tenen solucions que permeten, seguint l’analogia anterior, que grans del raïm d’un mateix carràs vagen a parar en la seua evolució a carrassos o, fins i tot, a ceps diferents!
Aquest canvi de plantejament és el que es va originar en els treballs de Poincaré. Tot i que poden rastrejar-se contribucions importants durant la primera meitat del segle XX, va ser a partir del anys cinquanta quan tota una sèrie d’investigacions multidisciplinars amb contribucions teòriques, numèriques i experimentals van portar a la necessitat d’acceptar: a) el determinisme més estricte és completament compatible amb la impredictibilitat més absoluta; b) sistemes d’innocent aparença per la seua estructura poden presentar comportaments veritablement perversos en la seua evolució temporal.
Un dels trets més característics que explica aquests fets és allò que s’anomena extrema sensibilitat a les condicions inicials de l’evolució dels sistemes. Això vol dir que una mateixa llei pot fer que dos sistemes preparats inicialment en estats pràcticament iguals acaben en la seua evolució, totalment determinista, en estats molt diferents. En expressió ben gràfica això és el que el meteoròleg Edward Lorenz va batejar com l’efecte papallona. I que, encara que ho puga semblar, no és simplement una coartada per als equips de predicció del temps en les televisions. El que vol dir és que, per exemple, l’oratge que farà en A pot dependre del fet que una papallona bata o no les ales en B. I si el lector és cinèfil pot recordar alguna imatge del film homònim de Colomo.
La reflexió que se’ns acut immediatament és: tot això està molt bé i pot ser molt entretingut, però és simplement un divertiment matemàtic i mera elucubració de teòrics? Certament no. Des del anys seixanta/setanta del segle passat tot un seguit d’estudis i experiments han detectat comportaments d’aquest tipus en una gran multitud de sistemes i fenòmens. En la ciència, com en tantes altres esferes de l’activitat humana, les modes imposen el seu domini. Durant els anys setanta i vuitanta es va publicar un allau de treballs que descobrien situacions caòtiques pertot arreu. Tant és així que fins i tot hom podria arribar a pensar si no seria pura casualitat que les prediccions de la ciència clàssica de tants i tants fets observacionals hagueren tingut èxit.

Figura 1: Poincaré i la portada de la seua famosa memòria. En realitat correspon a una revisió del treball originalment premiat.
Evidentment resulta una exageració pensar així. I això per diverses raons. En primer lloc hem associat la idea de comportaments caòtics a l’evolució temporal de sistemes i fenòmens. Però, de vegades, per tal d’observar comportaments d’aquest tipus cal deixar passar un temps extraordinàriament llarg. O siga, que, a curt termini, d’una durada que la mateixa teoria permet estimar, encara tenen sentit les prediccions convencionals. Hi ha una segona consideració que fa que es puga encara confiar en el poder predictiu de molts models físics o d’altres ciències. Com hem dit, el comportament caòtic amb la impredictibilitat que comporta constitueix una possibilitat, mai una necessitat. L’evolució temporal d’un sistema es tradueix, dins d’una teoria donada, en unes equacions en les quals figuren també uns paràmetres dels quals depenen les solucions. I, de vegades, una mateixa equació origina solucions qualitativament diferents (regulars unes, caòtiques les altres) segons els valors que prenguen aquests paràmetres. D’aquests fenòmens se’n diu bifurcacions.
Més amunt hem mencionat que en àrees molt diferents de l’activitat científica en el darrer quart del segle XX s’han detectat fenòmens caòtics i s’han elaborat models basats en les idees del caos per explicar-ne d’altres. Encara que només siga en titulars, donem una llista representativa. Com que els conceptes bàsics van sorgir en un context matemàtic, no és estrany que foren les ciències més matematitzades, l’astronomia i la física, els primers camps d’aplicació.
En el cas de l’astronomia s’ha estudiat l’estabilitat del sistema solar. En particular, s’ha determinat que Hyperion, un satèl·lit de Saturn, té en l’actualitat un moviment caòtic i es pensa que molt probablement tots els satèl·lits de forma irregular han passat en la seua història per èpoques de moviments irregulars. Això valdria per a Fobos i Deimos, de Mart, i Nereida, de Neptú. La distribució d’asteroides, o més ben dit la seua absència allà on s’esperen, també s’explica per anàlisis d’inestabilitats i caos.
En física l’espectre d’aplicacions és amplíssim. Oscil·ladors en sistemes mecànics, circuits electrònics, corrents de convecció, turbulències, sistemes acústics i òptics no-lineals… En química hi ha tot un camp del que s’anomenen oscil·ladors químics, que són reaccions en les quals les concentracions dels productes van variant de manera totalment erràtica, i en casos particularment vistosos això es tradueix en una dansa impredictible de colors.
En sistemes biològics s’han estudiat poblacions que, en determinades circumstàncies del seu medi ambient, poden evolucionar caòticament. En fisiologia també s’han utilitzat idees basades en la teoria del caos per analitzar electroencefalogrames o electrocardiogrames. Fins i tot en ciències socials, on la matematització és molt més recent i/o menys habitual, es construeixen models deterministes que expliquen comportaments d’aspecte aleatori. L’estudi de mercats financers n’és un exemple.
«Sistemes d’innocent aparença per la seua estructura poden presentar comportaments veritablement perversos en la seua evolució temporal»
En parlar de la presència de comportaments caòtics en sistemes reals convé fer una matisació. Per les seues connotacions amb el significat ordinari del terme algun lector pot pensar que aquests tipus d’evolució han de ser evitats. D’ací la importància de saber quan (és a dir per a quines condicions inicials i/o per a quins valors dels paràmetres) un sistema evolucionarà caòticament. Això pot ser cert en algunes aplicacions. Però no sempre és així. En molts casos es pot fer un ús, diguem-ne, positiu, del caos. Pot permetre, per paradoxal que semble, estabilitzar làsers i circuits electrònics, neutralitzar arítmies cardíaques en animals, i fins i tot transmetre missatges de manera segura.
Hem exposat, bé que esquematitzades al màxim i desproveïdes de tota vestimenta formal, algunes de les idees que formen el nucli central de la teoria del caos, les seues lleis i les seues aplicacions. Òbviament hem omès molt més del que s’ha dit: caos espacial, relació amb la geometria fractal, caos quàntic,… Sense més precisió tècnica resulta gairebé impossible entrar en discussions més concretes. I la teoria no està encara ni de bon tros tancada. De fet no hi ha una única definició universalment acceptada de caos i fins i tot quan se n’accepta una de concreta, no resulta gens fàcil demostrar que rigorosament un sistema la satisfà. De vegades es tenen moltes evidències però no una demostració irrefutable. El famós atractor de Lorenz ha estat tota una vida il·lustrant el caos en portades de llibres, revistes especialitzades i premsa en general. Només l’any 1999 el matemàtic suec Tucker ha demostrat el seu pedigrí caòtic.
Per anar acabant, ultra les ressonàncies més o menys exòtiques que el nom pot suggerir, hi ha una sèrie de característiques que ajuden a explicar l’interès que des dels finals dels anys setanta desperten els temes relacionats amb el caos. Heu-ne ací algunes:
— Toca aspectes sempre atractius en la divulgació de les idees de la física com ara determinisme, predictibilitat… És cert que aquestes són també referències habituals en discussions de mecànica quàntica, però en el caos determinista el debat es planteja en forma més paradoxal, car no s’ha d’abandonar l’esquema newtonià més familiar.
— Els estudis en aquesta àrea conjuminen a nivell fonamental, i no simplement instrumental, tècniques i resultats experimentals i analítics amb tractaments numèrics, de simulació i representació gràfica. I això ha contribuït a reconèixer un status a l’ús dels ordinadors molt més elevat que l’habitual paper de simple eina auxiliar que normalment se’ls atribueix.
— Un atractiu especial potser li ve al caos del seu marcat caràcter interdisciplinar repetidament comentat.
— Hom pot fer una idea relativament acurada des del punt de vista tècnic amb un modest bagatge matemàtic, tot i que les anàlisis poden després complicar-se seriosament i perillosa.
— Sense recórrer a inversions espectaculars poden realitzar-se experiments científicament significatius. I això és important! Hom diria que sense sortir de la cantonada és possible construir-se un circuit caòtic. I qui no ha vist aquells pèndols de mil formes que oscil·len sense solta ni volta?
Déiem al principi que l’Alcover-Moll il·lustrava l’ús de la paraula caos amb cites de Llull i Verdaguer. I ja que estem en el centenari de la mort de mossèn Cinto, podem acabar recordant de L’Atlàntida que “renàixer sembla el caos, sepulcre i bres dels mons”.






