| Era el 18 de setembre de 1783 a Sant Petersburg. L’home va fer classe de matemàtiques als seus néts. Després va fer uns càlculs a la pissarra i més tard es va reunir amb Lexell i Fuss per discutir sobre el recentment descobert planeta Urà. A les cinc de la tarda es va asseure i digué: «M’estic morint». Efectivament, a les set de la tarda d’aquell mateix dia moria el famós científic Leonhard Euler, de qui enguany commemorem el tres-centè aniversari del seu naixement.
Euler és considerat com un dels matemàtics més prolífics de la història, ja que, al llarg de 873 memòries i llibres, va contribuir al desenvolupament de la hidràulica, la hidrodinàmica, la teoria dels vaixells, l’elasticitat i la mecànica dels cossos rígids, així com a la teoria de nombres, de les sèries infinites, al concepte de funció, a les funcions de variable complexa, a les equacions diferencials, al càlcul de variacions, a l’astronomia, etc. L’estadística sobre la quantitat d’obres publicades per Euler és impressionant. Les seves obres completes contenen 25.000 pàgines, es divideixen en quatre grans parts o sèries i cadascuna té uns quants volums. Tanmateix si el pes relatiu quantitatiu és considerable no ho és menys, com exposarem, el seu pes qualitatiu. Euler va nàixer el 15 d’abril de 1707 a Basilea, en el si d’una família vinculada a la fe calvinista; tant el seu pare com el seu avi en van ser ministres. Va entrar a la Universitat de Basilea als tretze anys i va estudiar matemàtiques amb Johann Bernoulli. Les seves primeres publicacions són de quan tenia dinou o vint anys. Ja el 1727 va obtenir el segon premi en un concurs sobre temes d’investigació convocat per l’Académie des Sciences de París. En el seu treball estudiava la manera més eficient de col·locar els pals en un vaixell. El 5 d’abril de 1727 va abandonar Basilea per incorporar-se a la recentment inaugurada Acadèmia de Ciències a Sant Petersburg. D’aquesta primera etapa assenyalarem dos fets: el seu matrimoni a finals de 1733 amb Katharina Gsell, filla del pintor suís G. Gsell, amb qui va tenir tretze fills, cinc dels quals van morir essent infants, i la pèrdua de l’ull dret el 1738. No va tornar mai més a Basilea i va passar els anys successius entre dues estades a Sant Petersburg (1727-1741 i 1766-1783) i una a Berlín (1741-1766). En la seva primera estada a Sant Petersburg, va treballar a l’Acadèmia de Ciències, fundada el 1725 per Caterina I de Rússia, on Euler impartia classes i col·laborava en l’organització. Aquesta Acadèmia, creada seguint el model francès de l’Acadèmie des Sciences de París, representava la política científica del Govern. Aquestes societats del segle xviii eren finançades per la corona, que intervenia de manera directa en el seu funcionament. Tenien les seves pròpies instal·lacions i biblioteques i eren independents de les estructures universitàries. Euler participava activament en els projectes que el Govern encomanava a l’Acadèmia per trobar solucions a problemes tecnològics, com ara el disseny de mapes o bé la construcció de vaixells, encara que les seves principals contribucions van ser matemàtiques: anàlisi, teoria de nombres i mecànica. El 1741 ja tenia preparats uns noranta treballs, dels quals va publicar 55, inclosos els dos volums de mecànica. També va donar a conèixer moltes de les seves contribucions en les actes de l’Acadèmia titulades: Commentarii Academiae scientiarum imperialis Petropolitanae. D’aquesta època són alguns dels seus resultats més famosos: la funció gamma, la funció beta, el nombre e o bé les sumes de sèries infinites. A la mort d’Anna Leopoldovna, regenta d’Ivan VI, el 1740, i en veure el seu futur incert (a causa, possiblement, de la seva condició d’estranger), el 1741, Euler va acceptar la invitació de Frederic II el Gran de Prússia per incorporar-se a l’Acadèmia de Ciències de Berlín, fundada per Leibniz el 1700. En arribar a Berlín, el país es trobava enmig d’una gran crisi i Euler va haver de donar classes particulars per mantenir la seva família. Així ho va fer amb la princesa Filippina Von Schwendt (noble dama parenta del rei Frederic) i aquestes lliçons, més endavant, varen ser publicades a Rússia en tres volums, el primer el 1768 i el darrer el 1772, amb el títol: Lettres à une princesse d’Allemagne sur divers sujets de physique et de philosophie. Aquesta obra, considerada com una de les primeres de divulgació científica, va tenir molt d’èxit i se’n van fer dotze edicions en el francès original, nou en anglès, sis en alemany, quatre en rus i dues en suec. També n’hi ha d’italianes, espanyoles i daneses. Encara que Euler treballava per a les dues acadèmies (la de Sant Petersburg i la de Berlín), el 1744 esdevingué el promotor de la transformació, junt amb Maupertuis, que n’era el president, de l’antiga Societat de Ciències en la Reial Acadèmia de Ciències i Belles Arts de Berlín. Va ser nomenat director de la classe de matemàtiques d’aquesta acadèmia i membre del seu comitè directiu; al mateix temps que dirigia la biblioteca, formava part de la comissió de revisió de publicació dels treballs científics. Durant aquest període, Euler va incrementar considerablement la varietat de les seves investigacions. Va competir amb D’Alembert i amb Daniel Bernoulli en l’establiment dels fonaments de la física matemàtica i va ser també protagonista de discussions rellevants amb Clairaut i d’Alembert sobre la teoria dels moviments de la Lluna i dels planetes. Alhora, Euler elaborà la teoria del moviment dels sòlids, creà l’aparell matemàtic de la hidrodinàmica, desenvolupà amb èxit la geometria diferencial de superfícies i estudià intensivament òptica, electricitat i magnetisme. Al llarg de la seva estada a Berlín va preparar no menys de 380 treballs, dels quals van ser publicats 275, incloent-hi diversos llibres llargs com ara una monografia sobre el càlcul de variacions (1744); un treball fonamental sobre el càlcul d’òrbites (1745); un treball sobre artilleria i balística (1745); un llibre d’anàlisi: Introductio in Analysin infinitorum (1748); un tractat sobre vaixells i navegació, preparat ja en una versió anterior a Sant Petersburg (1749); la seva primera teoria del moviment de la Lluna (1753); un volum de càlcul diferencial: Institutiones calculi differentialis (1755); i finalment, el tractat sobre la mecànica de sòlids: Theoria motus corporum solidorum seu rigidorum (1765). Entre 1740 i 1750 Euler va prendre part en molts debats i discussions sobre diverses temàtiques científiques i filosòfiques, com ara sobre les monadologies de Leibniz i de Wolff, sobre el principi de mínima acció de Maupertuis, sobre els logaritmes dels nombres negatius, sobre la solució de l’equació de la corda vibrant, sobre problemes òptics, etc. El 1759, Maupertuis va morir i Euler va esdevenir la figura de referència a l’Acadèmia sota la supervisió del rei Frederic II el Gran. Les diferències entre el rei i Euler eren molt àmplies, tant en el caràcter com en la manera d’entendre i valorar la ciència. El rei estimava la poesia i li semblaven poc pràctiques les matemàtiques; diuen que a Euler l’anomenava «ciclopi matemàtic». Quan el 1763 Euler va saber que el rei pensava nomenar D’Alembert president de l’Acadèmia, va escriure a Sant Petersburg i Caterina II la Gran li va fer una oferta per tornar-hi. De fet, D’Alembert no va acceptar, però altres conflictes de tipus financer, durant el 1765, entre Euler i el rei, el van decidir a anar-se’n i el 9 de juliol de 1766 va abandonar Berlín. En el seu retorn a Sant Petersburg va ser rebut amb grans honors, tot i que en arribar-hi va perdre totes les seves possessions en un incendi i, poc temps després, el 1773 va morir la seva dona. Tanmateix tres anys més tard es va casar amb la seva cunyada. En la seva segona etapa a Sant Petersburg l’acompanyaven tres dels seus fills. Un d’ells, Johann Albrecht, va esdevenir acadèmic, va ocupar la càtedra de física i, a partir de 1769, va ser nomenat secretari permanent de l’Acadèmia. Poc temps després d’instal·lar-se de nou a Sant Petersburg, una malaltia va deixar Euler completament cec; no podia llegir i escrivia amb guix en una pissarra amb grans lletres. Malgrat la ceguesa, les seves activitats científiques no van cessar. La seva memòria era fantàstica i tenia molts ajudants, entre ells els seus fills i alguns deixebles i acadèmics que ell convidava. Tot sovint, dictava els seus treballs, però la majoria de les vegades s’establia una discussió i Euler desenvolupava les seves idees, calculava mentalment taules i donava exemples. Així, les 775 pàgines de Theoria motuum lunae… (1772) van ser completades amb l’ajuda del seu fill Albrecht i els acadèmics Krafft i Lexell, que se citen en el títol del llibre. Krafft també el va ajudar en els tres volums de Dioptrica (1769-1771). Els articles d’Euler de la segona estada a Sant Petersburg eren breus per causa de la ceguesa. Tot i això va publicar els tres volums d’Institutiones calculi integralis (1768-1770), les principals parts de la qual ja havia acabat a Berlín. També va publicar una versió abreujada de Scientia navalis. Théorie complète de la construction et de la manoeuvre des vaisseaux (1773), que va ser traduïda a l’anglès, italià i rus, i que li va proporcionar grans sumes dels governs rus i francès. Fuss, jove suís convidat per Euler, el va ajudar a preparar l’obra Éclaircissements sur les établissements publics… (1776), que va ser molt influent en el desenvolupament de les assegurances: moltes companyies empraven els seus mètodes de solució i les seves taules. Euler va continuar participant en altres funcions a l’Acadèmia de Sant Petersburg. Junt amb el seu fill, era membre de la comissió que dirigia l’Acadèmia, encara que el 1774 van deixar-ho, a causa de les seves diferències amb Orlov, que n’era el president. Euler va treballar fins l’últim dia de la seva vida i immediatament després de morir va rebre nombrosos homenatges per part de l’Acadèmia de Sant Petersburg, de l’Académie de Sciences de París i de la comunitat científica europea. Les seves restes mortals es troben a Sant Petersburg. En el seu treball, Euler presentava les matemàtiques connectades amb les aplicacions a altres ciències, a problemes tecnològics i a la vida pública. Les seves contribucions abracen els coneixements de les matemàtiques pures i les matemàtiques mixtes que es troben a la classificació de les matemàtiques del 1754 de l’Encyclopédie de D’Alembert. Els enciclopedistes havien recollit les idees i la classificació de Francis Bacon del 1605 de les matemàtiques en matemàtiques pures, la geometria i l’aritmètica, i en matemàtiques mixtes, la perspectiva, la música, l’astronomia, la cosmografia, l’arquitectura, l’enginyeria, etc. Per aquest motiu no ens ha d’estranyar que Euler, com a bon il·lustrat, treballés en un gran ventall de temàtiques que avui identifiquem com a diferents disciplines o, fins i tot, com a disciplines independents de les matemàtiques. Euler era un creador, en les seves contribucions va intentar obrir nous camps, i així va donar a conèixer nous símbols com el nombre e per representar la base dels logaritmes, el nombre i per representar els complexos, la lletra F i els parèntesis per a les funcions; també va donar noves definicions, noves fórmules, nous polinomis (anomenats d’Euler), integrals eulerianes, línies d’Euler, etc. No obstant això, les seves contribucions van ser decisives sobretot en tres àrees: en el càlcul de diverses variables, especialment aplicat a la física amb la introducció de les equacions amb derivades parcials; en la teoria i aplicació de les equacions diferencials ordinàries i, finalment, en l’ús dels mètodes analítics o de l’àlgebra en la teoria de nombres. Euler va ser un creador de nocions i mètodes molt importants dins les matemàtiques pures i mixtes, encara que en molts casos el valor d’aquestes contribucions ha estat reconegut molts anys després de la seva mort. Efectivament, molts treballs matemàtics desenvolupats en el segle xix es van fonamentar en els resultats obtinguts anteriorment per Euler. Euler va ser un gran mestre i també un magnífic divulgador. Quan exposava ho feia amb senzillesa i explicava el camí recorregut fent observacions sobre els intents, tant si eren fructífers com si no. A tall d’exemple adjuntem alguns dels seus comentaris a l’hora de deduir el valor de la funció beta B (3/2, 3/2) en un text que va publicar el 1730 a Comentarii academiae scientiarum imperialis Petropolitanae, a Sant Petersburg, titulat: «De progressionibus transcendentibus, seu quarum termini generales algebraice dari nequeunt» (“Sobre progressions transcendents, és a dir, aquelles que els seus termes generals no poden ser expressats algebraicament”). En aquest text, Euler, al llarg de 29 apartats, vol trobar el terme general d’una progressió formada pels termes 1, 2, 6, 24, …, és a dir, n!, i remarca la seva preocupació, ja que sap que no pot ser expressat algebraicament per a tots els valors de n. Veiem com Euler raona que és possible, doncs, que el terme general d’aquesta progressió no tingui només termes algebraics, sinó també termes que depenen de quadratures (expressió emprada per designar el que avui anomenem àrees o integrals definides). «Jo havia prèviament suposat que el terme general de les sèries 1, 2, 6, 24,… podia ser donat, si no algebraicament, com a mínim exponencialment. Però, després d’haver vist que alguns termes intermedis depenen de la quadratura del cercle, vaig reconèixer que ni quantitats exponencials ni algebraiques són adequades per expressar-ho. Per al terme general d’aquesta progressió s’han d’incloure altres quantitats que depenen de la quadratura del cercle o d’altres quadratures, però que no poden ser representades per cap fórmula algebraica o exponencial. Em preguntava de quina manera les fórmules diferencials serien apropiades per expressar el terme general de la progressió. Un terme general ha de tenir n per substituir i trobar els termes. Però una fórmula diferencial ha de contenir alguna quantitat variable. No té sentit prendre n, n no és la variable d’integració, sinó que, després que la fórmula hagi estat integrada, n hauria de servir per a la formació de la progressió.» [Euler, 1730, 39] Euler raona com farà la demostració, més endavant mostra un camí amb el qual no troba la solució i també en raona els motius. Llegir Euler és aprendre, no únicament aprendre amb el desenvolupament dels seus resultats, sinó també en llegir les seves explicacions i raonaments quan el camí que emprèn no és profitós. Així doncs, el nostre millor suggeriment pot ser, seguint les paraules de Laplace: «Llegiu Euler, ell és el mestre de tots nosaltres.» BIBLIOGRAFIA Obres d’Euler en línia: |
El gran matemàtic Leonhard Euler. «Amb els seus 873 llibres i memòries, Euler és considerat com
Portada de la Introductio in Analysin Infinitorum (1748). «“Lettres à une princesse d’Allemagne”
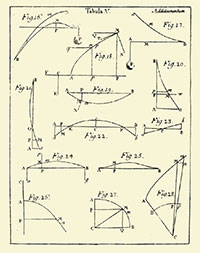
Làmina amb figures a Methodus Inveniendi, (1748). «Poc després de tornar a Sant Petersburg, una malaltia el va deixar cec. Malgrat això, les seves activitats científiques no
|
Leonhard Euler (1707-1783): l’home, el creador i el mestre