Autoorganització fluidodinàmica

An almost Exclusively Aesthetic Approach to Self-organising Fluid Dynamics. In this article the author illustrates self-organisation in some fluid dynamic systems, paradigms of complexity. Their complexity can only be approached on an almost exclusively aesthetic level. The evolution of fluid flows, the widely varied instabilities and transitions that are known to exist, turbulence… offer a vast panorama within which, in spite of the progress made, much has yet to be understood.

Al mestre Tomás Marco
en el seu seixantè aniversari

Introducció

Una bifurcació és una reestructuració qualitativa, suau o abrupta, d’un sistema dinàmic evolutiu que es produeix quan un dels seus paràmetres, modificat des de l’exterior o potser espontàniament, adopta un valor “crític”, també denominat valor llindar d’inestabilitat o bifurcació. Cal separar les etapes de desenvolupament dels moments de transició, en ocasions dits crítics, en els quals una inestabilitat pot conduir a una nova forma i/o nova funció. En el primer cas podem limitar-nos, bàsicament, a lleis deterministes, encara que el sistema experimente contínuament fluctuacions que intenten desestabilitzar-lo. Aquí petites variacions en causes originen petits efectes i, generalment, les fluctuacions decauen. En un punt crític els elements estocàstics (l’atzar, les fluctuacions) intenten predominar sobre els deterministes i un canvi suau pot donar un efecte dràstic. Determinisme (necessitat) i fluctuacions (atzar) fan evolucionar el sistema.

«Sistemes tan dispars com el ferromagnetisme, l’emissió de llum per un làser o el comportament sociològic d’animals i humans són descrits, actualment, amb una metodologia de valor universal»

Les fluctuacions, espontànies o forçades, permeten explorar contínuament noves possibilitats, nous estats a què poder arribar i en els quals estabilitzar-se d’acord amb els lligams externs. La “selecció” té sentit intuïtiu si entre aquests estats n’hi ha algun d’abast més ràpid que els altres, o d’estabilitat relativa major, o té una estructuració o funció menys costosa, o ha estat afavorit per alguna causa externa (que pot ser subtil i que és el seu caire o vici de naixement), però no sempre parlar de selecció té sentit. Si una fluctuació passa el nivell llindar d’inestabilitat i s’estableix fins dominar qualsevol altra possibilitat o fluctuació del sistema, llavors l’estat de partida desapareix perque ja és inestable, i el nou estat pren el relleu en l’evolució.

Els estats o fases d’un sistema, els seus “atractors”, punts fixos, cicles límit o trajectòries quasiperiòdiques, es caracteritzen perquè podem predir el futur qualsevol que siga l’interval de temps considerat; generalment, dues trajectòries inicialment pròximes no se separen apreciablement al llarg del temps. Aquests atractors eren els únics coneguts fins a l’últim terç del segle XX, quan, a partir d’una observació de B. Saltzman, el meteoròleg E. N. Lorenz, estudiant amb computador l’evolució de les trajectòries d’un model molt simplificat de la convecció atmosfèrica, va descobrir un exemplar d’atractor aperiòdic, caòtic (de pas diguem que amb dimensió fractal, entre dos i tres). Simultàniament al descobriment “experimental” de Lorenz, i amb independència d’aquest, l’existència d’atractors caòtics i la seua estabilitat van ser establertes per A. N. Kolmogoroff, S. Smale, D. V. Anosov, Ya. G. Sinai, B. Mandelbrot, D. Ruelle, F. Takens i L. P. Shilnikoff, entre altres. Smale va proposar una transformació topològica que, com si pastara pa, permet visualitzar el caràcter erràtic de les òrbites en un atractor aperiòdic.

Varietats de fenòmens i universalitat de conceptes i models

H. Haken va establir una visió unificada de la molt diversa fenomenologia dels sistemes complexos i de la seua evolució abans esbossada. Sistemes tan dispars com el ferromagnetisme, l’emissió de llum per un làser, l’autoorganització fluidodinàmica, química o bioquímica (teixits espacials, rellotges químics o biològics, etc.), el comportament ecològic i fins i tot sociològic d’animals i humans són descrits, actualment, amb una metodologia de valor universal. La idea seminal prové de L. D. Landau, qui va imaginar que la molt diversa fenomenologia de les transicions en equilibri termodinàmic es podria descriure universalment si, prescindint dels detalls, ens concentrem en l’evolució d’una, o unes poques, magnituds que va denominar modes dominants, paràmetres d’ordre o d’autoorganització. Haken va estendre el concepte als processos molt allunyats de l’equilibri establint que l’evolució d’aquests modes, en el temps i en l’espai, dicta el comportament sinèrgic del sistema, per molt complex que siga. Tot seguit ens limitarem a il·lustrar fenòmens d’autoorganització en alguns sistemes fluidodinàmics que certament són paradigmàtics de la complexitat.

Figura 1: Cel·les convectives de Bénard. Quan s’escalfa per la base un líquid, per exemple un oli de silicona o qualsevol altre líquid viscós, a causa de la flotabilitat d’Arquímedes o de l’efecte de la variació de la tensió superficial líquid-aire, o de la combinació simultània d’ambdós mecanismes, el sistema evoluciona des d’una situació homogènia (sense ordenar) i es va autoorganitzant en cel·les de diverses formes, com ara les hexagonals. La seqüència permet veure com, a causa de la presència de la paret cilíndrica, s’intenta produir una forma axisimètrica, però a l’últim la dinàmica intrínseca del líquid domina i indueix la formació d’una bresca d’abella.

Formes convectives estacionàries

La figura 1 mostra el naixement d’un teixit espacial en cel·les convectives, en una capa o pel·lícula de líquid escalfada per la base i oberta a l’aire ambient. La figura 2 (vegeu també la figura 3) dóna les línies de corrent en una cel·la. S’hi pot observar que les “molècules” semblen seguir-se les unes a les altres.

Aquestes cel·les, i altres formes convectives anàlogues, són conseqüència d’un o dos mecanismes capaços d’induir en una pel·lícula líquida, a l’atmosfera o a l’oceà, inestabilitat de l’estat de repòs quan el sistema és sotmès a la influència externa d’un escalfament o d’adsorció o de desorció (inclosa l’evaporació) d’un tensioactiu (molècules actives en una superfície) si posseeix una superfície lliure o té interfície amb un altre líquid.

Va ser H. Bénard qui, en la seua tesi doctoral (París, 1900), va deixar experimentalment establerta l’autoorganització fluidodinàmica en aquestes cel·les convectives que avui porten el seu nom. Lord Rayleigh (1916) va atribuir, erròniament però genialment, l’excitació de les dites formes (generalment hexagonals) a una inestabilitat produïda per la flotabilitat d’Arquímedes (quan un fluid s’escalfa per la base condueix a una situació en què el cap és pesant i els peus i les cames, lleugers; és, per tant, una situació mecànicament inestable). Aquest mecanisme afavoreix la formació de certs núvols i, en particular, els carrers de núvols quan hi ha vent. És el mecanisme subjacent al model atmosfèric estudiat per Lorenz.

El que passa en una pel·lícula líquida escalfada per la base i oberta a l’aire ambient, com és el cas d’un oli de silicona en la figura 1 (i en els experiments de Bénard), és que la tensió superficial líquid-aire es veu afectada pel dit escalfament. Com que l’esmentada tensió, s, depèn de la temperatura, si algun punt està més calent que el seu entorn el seu valor cau i llavors s’inicia un moviment cap a més fred (efecte explicat per C. Marangoni), perquè s és a la superfície (excepte el signe) el que la pressió al volum del líquid. En desplaçar-se líquid cap a la superfície, el “buit” és reomplit amb líquid que ve de baix, que està encara més calent… de manera que la fluctuació inicial tendeix a reforçar-se. No obstant això, com que un líquid real és viscós, la viscositat tracta de frenar aquest moviment. A més a més la difusivitat calorífica també tendeix a eliminar-la, encara que molt lentament (un centímetre en 103 s). Perquè es puguen veure les cel·les de Bénard, doncs, la diferència de temperatura entre la base calenta i la superfície superior freda ha d’adquirir un valor llindar que supere l’efecte de fre de la viscositat i la termalització (en la pràctica uns quants graus per mil·límetre o centímetre segons el líquid). La talla horitzontal d’una cel·la sol ser de l’ordre del gruix de la pel·lícula líquida. Idèntic mecanisme ocorre quan en comptes d’escalfar el líquid, hi actua un tensioactiu. La figura 2 mostra l’autoorganització “molecular” en cel·les (com les de Bénard) observades lateralment.

Diversos aspectes del mateix fenomen, es poden il·lustrar tant experimentalment com numèricament. En particular, la figura 3 mostra l’evolució des d’una situació desordenada (la calor flueix només per difusió) a l’autoorganització en panells hexagonal (la calor flueix per difusió i convecció).

Fig. 3: Evolució numèrica (obtinguda per J. Bragard) des d’un estat desordenat, en què la calor només es difon per la llei de Fourier (vegeu figura 1), cap al panell convectiu hexagonal, on la convecció s’afegeix a la conducció, a causa de l’efecte de Marangoni per l’escalfament en la base d’una pel·lícula líquida.

Ones i solitons dissipatius

Vegem ara què passa si en comptes d’escalfar el líquid per la base, el refredem per la base o bé escalfem l’aire sobre la superfície lliure. L’experiment alternatiu consisteix a adsorbir un vapor lleuger (tensioactiu) i esperar fins que haja estat prou absorbit en el volum. Aquest és el cas de l’adsorció de vapor de pentà per una pel·lícula de toluè líquid que és més dens que el líquid pentà i té superior tensió superficial amb l’aire.

Si, de nou, imaginem un punt calent, com que quan es desplaça arrossega des del volum líquid més fred o més dens, la fluctuació inicial de moviment convectiu tendeix a desaparèixer; és el procés ondulatori o de sobreestabilitat, com si d’un pèndol es tractara, que condueix a oscil·lacions (cicles límit), possible formació d’ones superficials i, amb el temps, internes, ja que la pel·lícula líquida per escalfar-se en el cap o absorbir un lleuger vapor s’estratifica establement. En superfície les ones es denominen capil·lars (capil·larogravitatòries en presència de gravetat) o dilatants (a causa de l’aparent compressió-expansió que s’hi observa). En el volum, a l’atmosfera i a l’oceà, se les denomina ones (internes) de Brunt-Väisälä, en honor dels científics que, pionerament, les van descriure.

Figura 4: Trens d’ones induïts en una pel·lícula líquida escalfada per l’aire: a) recipient cilíndric circular; b) recipient anul·lar cilíndric circular. La visualització és per ombroscopia, que envia llum de baix cap amunt. El sentit de gir a esquerres o dretes és arbitrari i, en principi, equiprobable.

Les figures 4 i 5 il·lustren fenòmens ondulatoris observats al laboratori (cinemàticament) idèntics a ones en la naturalesa, en canals d’aigua, descrites a mitjan segle XIX per J. S. Russell i després per H. Bazin, i, poc més tard, per E. Mach i col·laboradors, al laboratori amb xocs gasosos (així com en ressalts hidràulics per diversos autors més). Aquests fenòmens, parcialment però clarividentment estudiats per J. Boussinesq, Lord Rayleigh, D. Korteweg i G. de Vries, a finals del segle XIX, van ser després redescoberts per N. Zabusky i M. Krustal (1965), integrant numèricament equacions d’ones extretes mitjançant apropiades simplificacions de les equacions fluidodinàmiques. Els autors esmentats van introduir el concepte de solitó en fluids ideals, sense viscositat, perquè tant en col·lisions frontals o d’angle arbitrari com en reflexions en parets aïllades, dites ones (ona solitària de Russell, per exemple) es comporten (clàssicament, en imatge inversa de la quàntica) més com a partícules (electró, protó, etc.) que com a ones. El concepte de solitó prompte va adquirir universalitat i va obrir un camp de la matemàtica aplicada. Les figures 4 i 5 mostren solitons dissipatius. Ones solitàries, solitons i ressalts (solitònics) apareixen en diverses situacions atmosfèriques, en rius (de diversos metres d’altura: mascaret del riu Sena o bore del riu Severn) i en estrets (com en la pycnoclina de l’estret de Gibraltar, on poden assolir fins a cent metres d’amplitud encara que siguen apenes perceptibles a la superfície del mar) o a l’oceà (el tsunami és una onada gegantina en un port que ocorre com a etapa final d’una ona solitària que ha recorregut de tres a quatre mil quilòmetres a uns vuit-cents quilòmetres per hora, per exemple d’Alaska a Hawaii). L’impuls nerviós, potencial d’acció o espiga neuronal és un solitó dissipatiu que pot viatjar en axons com el del calamar a uns quatre-cents quilòmetres per hora, pràcticament sense deformar-se.

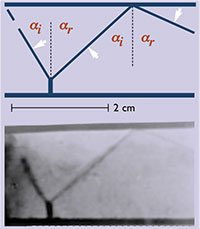
Figura 5: Doble reflexió normal (αi≈αr) i anòmala, típicament solitònica, amb braç de Russell-Mach. Visualització per ombroscopia.

Perspectiva

Després de comentar molt succintament l’evolució dels sistemes dinàmics complexos (que, encara que no ho hem dit, solen estar regits per lleis alineals, bucles de realimentació positiva o negativa, retardaments en la transmissió de senyals, etc.), hem descrit alguns casos d’autoorganització fluidodinàmica regida per les equacions d’evolució de Navier-Stokes, Fourier i Fick amb les seues corresponents condicions de contorn (i inicials segons els casos) i equacions d’estat o constitutives (de volum o de superfície). De la seua complexitat només hem donat una aproximació quasi exclusivament estètica, acostant la brasa a la nostra “sardina”. L’evolució dels corrents fluids, les molt diverses inestabilitats i transicions que entre aquests es coneixen, la turbulència a penes dissipativa (O. Reynolds, Kolmogoroff), la turbulència interfacial molt dissipativa… ofereixen un vast panorama en què fins i tot havent-hi molt entès queden qüestions bàsiques per entendre. Algunes semblen impossibles d’aprehendre amb capacitat predictiva tal com ocorre amb l’atmosfera, si pensem en el temps més enllà d’uns pocs dies.