
From Zebras to Dunes and Other Things. Dissipative Structures in our Natural Environment. Spatial structures, like striped or hexagonal patterns, are widespread in nature and are to be found in systems as unconnected as the beach sand, the patterned fur of certain animals, the clouds or the light emitted by certain optical systems. The ubiquity of these dissipative structures, which is how they are known, is not accidental but shares common components that allow a universal description of their origin and evolution.
La següent afirmació és òbvia: una zebra no és una duna de sorra. No obstant això, les dunes, com els fons dels rius o certes agrupacions de núvols, presenten ondulacions regulars similars a la decoració llistada de la zebra, o d’alguns peixos i insectes. Així, si el “és” de la primera afirmació el restringim, grosso modo, a les formes o patrons, aquella deixa de ser òbvia, perquè, de fet, zebres i dunes resulten “ser” iguals.
És tot això només parlar per no callar? La resposta seria afirmativa si no poguérem dir res més però, per sort, o potser per desgràcia per al lector, aquest article s’estén un poc més per intentar explicar que zebres i dunes “són” iguals.
«Crida l’atenció que un sistema químic i un de biològic puguen ser classificats dins d’una mateixa categoria»
La pregunta pertinent és si podem comprendre unificadament la formació de patrons llistats en sistemes de natura tan dispar com els abans esmentats. Admetem que una cosa s’entén quan es pot modelitzar matemàticament mitjançant un conjunt d’equacions les solucions de les quals reprodueixen allò observat. Idealment, els models permeten predir nous comportaments que, tanmateix, s’observen en experiments controlats. Doncs bé, aquests models existixen –després en parlarem– i prediuen resultats d’experiments concrets.
Seguint amb els patrons llistats, hi ha multitud de sistemes experimentals que els exhibixen. Valga com a exemple els sistemes de reacció-difusió en química i biologia, entre els quals podem mencionar la reacció CIMA (chlorite-iodide-malonic acid) entre rebosts de reactius contínuament renovats, o el creixement de poblacions de bacteris (com ara Escherichia coli, Salmonella typhimurium o Bacillus subtilis) sota el subministrament controlat de nutrients.
Crida l’atenció que un sistema químic i un de biològic puguen ser classificats dins d’una mateixa categoria. En el cas que ens ocupa això vol dir que la dinàmica que condueix a la formació de patrons en ambdós sistemes ve regida pels mateixos fenòmens bàsics: reacció i difusió. Per descomptat, en un cas la reacció involucra reactius químics i en l’altre nutrients i éssers vius. Però resulta encara més sorprenent el fet que tant sistemes de reacció-difusió, com altres sistemes en els quals no existeixen reacció o difusió o cap de les dues (com ara la convecció de Rayleigh-Bénard en fluids, o la llum emesa per sistemes òptics no lineals), siguen descrits, en condicions adequades, per equacions iguals. Això vol dir que existeix una universalitat en el fenomen de la formació de patrons espacials i que els detalls microscòpics (en el sentit dels processos elementals que ocorren en un sistema particular) perden relleu en favor de lleis macroscòpiques què governen el sistema com un tot. És a dir, les estructures macroscòpiques són la manifestació d’un comportament col.lectiu sinergètic, resultat de la cooperació i la competició de la dinàmica dels elements microscòpics.

Figura 2: Les tres primeres figures corresponen a la superfície d’una capa prima d’oli de silicona sotmesa a una vibració vertical. En a la freqüència de vibració és de 30 Hz i s’aprecia un patró hexagonal, en b i en c (29 i 27 Hz respectivament) s’aprecien diferents tipus de quasicristalls. En d s’aprecien dos tipus de patrons hexagonals obtinguts a partir d’un model de vàlvula de cristall líquid. En e es mostra un patró hexagonal experimentalment obtingut en un dispositiu en el qual una capa prima de sorra és sotmesa a vibració vertical.
La universalitat de la qual parlem no es restringeix, però, als patrons llistats, si no tot això seria molt avorrit! Un mateix sistema, sotmès a condicions diferents, pot desenvolupar patrons més complicats com ara estructures hexagonals, ròmbiques, quasicristal·lines, estructures localitzades (solitons, oscil·lons, breathers, etc.) o fins i tot comportaments turbulents (caos espaciotemporal). Des del punt de vista de la modelització, ocorre el mateix: un mateix model, depenent del valor numèric que s’assigne als paràmetres que hi apareixen (i que és on es registra, bàsicament, la informació sobre el sistema particular) permet reproduir els diversos patrons que s’observen en els sistemes reals.
Quina és, llavors, la base de la qual hem de partir per a modelitzar aquestes estructures? Si el que volem és una descripció universal, hauria de ser prou, per tal de comprendre la formació, evolució i les propietats dels patrons, tenir en compte un conjunt d’elements genèrics que han de ser necessàriament comuns a sistemes tan dispars. En aquesta descripció es caracteritza l’estat del sistema mitjançant una funció de l’espai i el temps, usualment anomenada paràmetre d’ordre, i es construeix l’equació que governa la seua evolució. A partir del paràmetre d’ordre és possible determinar l’evolució de la distribució espacial de les magnituds d’interès d’un problema particular (les concentracions de reactius, la població de bacteris, la llum emesa per un làser, la distribució de pigments en la pell de la zebra, etc.). Per descomptat, aquestes lleis universals haurien de poder ser obtingudes a partir de les lleis microscòpiques específiques de cada sistema.
Quins són aquests elements que comparteixen els sistemes formadors de patrons que han de ser incorporats en la seua descripció unitària? Un tret comú a tots els sistemes esmentats és que són dissipatius i es troben fora de l’equilibri. És a dir, són sistemes oberts què interaccionen amb l’entorn i guanyen i perden energia contínuament. Per això, als patrons que hi apareixen se’ls anomena, genèricament, estructures dissipatives. Hi ha més ingredients en el problema, però, per tal d’entendre’ls, haurem de parlar amb una miqueta més de detall. Vejam.
L’evolució espaciotemporal de qualsevol sistema ve regida per un conjunt d’equacions diferencials que determinen unívocament l’estat del sistema en un instant qualsevol a partir d’unes condicions inicials. Quan les equacions d’evolució del sistema són lineals, és a dir, quan les variables apareixen en elles multiplicades únicament per constants, regeix l’anomenat principi de superposició. En virtut d’aquest, qualsevol combinació lineal de solucions de les equacions és al seu torn una solució. En termes més físics, això implica que en un sistema lineal l’efecte últim de l’acció combinada de dues causes diferents és la mera superposició dels efectes de cada causa presa individualment. Així, el principi de superposició impedix que el sistema exhibesca comportaments inesperats de caràcter sinergètic. Resulta essencial, doncs, que la interacció tinga un caràcter no lineal per tal que la cooperació o la competició entre els elements constituents puga tenir lloc. Però com apareix la no-linealitat en els sistemes?
«Existeix una universalitat en el fenomen de la formació de patrons espacials»
En realitat hi ha poques lleis realment lineals en la natura. Que una llei siga lineal significa que existeix una proporcionalitat exacta entre causa i efecte: a valor doble de la causa correspon un valor doble de l’efecte. El caràcter lineal de les lleis sol ser, però, una aproximació. Considerem, per exemple, una molla: si no hi exercim cap força, està en repòs, que és l’estat d’equilibri. Si ara allarguem la molla veiem que apareix una força de reacció que tendeix a escurçar-la i, per tant, a tornar-la a la posició d’equilibri, i que apareix una oscil·lació en soltar-la. Quan el desplaçament és prou menut, la força li és proporcional (llei de Hooke) i és, per tant, lineal. Però quan el desplaçament no és tan menut la llei de Hooke ja no es verifica. En aquesta situació, per allargar-la el doble hem de fer una força què no serà el doble que abans: la força adquireix una dependència no lineal amb el desplaçament. Valga aquest exemple per a afirmar que la majoria dels sistemes és intrínsecament no lineal quan se’ls allunya prou de l’estat d’equilibri. Hi ha, però, altres formes d’introduir la no-linealitat, com ara mitjançant mecanismes de retroalimentació, amb els quals la causa modifica el seu valor en funció de l’efecte. Així doncs, la presència de termes no lineals en les equacions d’evolució dels sistemes no és, ni de lluny, un fenomen extraordinari. Respecte a la forma específica de la no-linealitat hi ha, no cal dir-ho, infinites possibilitats, però, sovint, aquella resulta relativament poc important en el sentit que sols modifica el detall dels resultats.
D’altra banda, com que les estructures dissipatives mostren un alt grau d’ordre espacial, és necessària l’existència d’algun mecanisme de transferència d’informació des d’un punt a un altre de l’espai. Dit d’una altra forma, és imprescindible que hi haja algun mecanisme de no-localitat. Exemples en són la difusió en sistemes químics o la difracció en sistemes òptics.
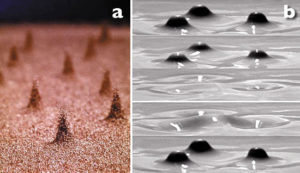
Figura 3: Estructures localitzades (oscil·lons) obtinguts experimentalment amb sorra, a, i aigua, b, vibrades verticalment. En b s’aprecia l’evolució dels oscil·lons al llarg d’un període de la seua oscil·lació.
Per últim, i com ja es va avançar, els sistemes dissipatius perden energia, cosa que fa que tendesquen a l’equilibri tèrmic, on totes les estructures desapareixen. Per això resulta imprescindible aportar energia al sistema per tal de mantenir-lo lluny de l’equilibri tèrmic, que és el domini en què la no linealitat pot provocar la ruptura espontània de simetria i fer aparèixer comportaments complexos.
Amb aquests elements (aportació i dissipació d’energia, no localitat i no-linealitat) es pot formular equacions d’evolució del paràmetre d’ordre, relativament senzilles, algunes de les quals, com ara la de Ginzburg-Landau o la de Swift-Hohenberg, representen el paper de paradigmes en ciència no lineal. Sovint aquestes equacions s’introdueixen a partir d’arguments purament heurístics. Això ha de ser així necessàriament quan es consideren sistemes molt complicats dels quals es desconeix el detall de les lleis microscòpiques que els regeixen (penseu, per exemple, en la formació d’estructures en colònies bacterianes). El mateix passa quan es tracta de sistemes en què les equacions microscòpiques, tot i que ben conegudes, són tan complicades que el seu estudi resulta inabordable. En aquests casos les equacions de paràmetre d’ordre representen, de facto, el paper de lleis que governen la formació de les estructures dissipatives. No deixa de ser sorprenent que les lleis microscòpiques puguen ser ignorades.
Afortunadament, en altres ocasions, les equacions de paràmetre d’ordre poden ser formalment deduïdes a partir de primers principis. Un exemple el constitueixen els sistemes òptics no lineals. Aquestes deduccions serveixen per a donar una base conceptual més ferma a les equacions de paràmetre d’ordre (que en aquests casos són deduïdes i no postulades), perquè mostren rigorosament el comportament sinergètic d’una multitud d’elements. Tot i això, no deixa de ser fascinant que quantitats ingents de partícules subjectes a les cegues forces de la natura siguen capaces d’organitzar-se en patrons d’activitat cooperativa descriptibles en termes d’un o uns pocs paràmetres d’ordre.
«Els sistemes macroscòpics autoorganitzats es comporten seguint lleis pròpies, pràcticament independents de les del nivell microscòpic»
Veiem, doncs, que en la ciència no lineal existeix un canvi d’enfocament respecte a la ciència tradicional, ja que, almenys en cert sentit, s’ha passat de l’enfocament analític què ha dominat la ciència des del Renaixement, a un enfocament més global, holístic, en què es considera el sistema com un tot.
Insistim en aquesta idea: un dels ensenyaments que podem extraure d’aquest canvi d’enfocament és l’oposició existent entre allò microscòpic, entès com la dinàmica individual de cada constituent d’un conjunt autoorganitzat, i la dinàmica del conjunt. La dinàmica microscòpica ve regida per lleis que depenen del tipus d’interacció particular (electromagnètica, química, mecànica, etc.) però aquest caràcter específic es dilueix en el comportament macroscòpic, ja que aquest ve regit per lleis universals. Per descomptat no és el mateix un sistema químic que òptic (ni una zebra que una duna), però la diferència apareix únicament en els coeficients de les equacions de paràmetre d’ordre i no en la seua estructura. Així els sistemes macroscòpics autoorganitzats es comporten seguint lleis que els són pròpies i que són pràcticament independents de les lleis específiques del nivell inferior d’organització, el nivell microscòpic.





