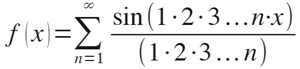Karl Weierstrass (1815-1897)

«Molts teoremes fonamentals de les branques de l’anàlisin porten el nom de Weierstrass, ja sigui perquè ell els va descobrir o per haver estat el primer a donar-ne una demostració completa i rigorosa»

Un dia qualsevol de 1873, a la Universitat de Berlín, els estudiants s’afanyaven a arribar puntuals a les sempre motivadores classes del professor Karl Weierstrass (1815-1897), considerat com el pare de l’anàlisi matemàtica. Molts teoremes fonamentals de les branques de l’anàlisi porten el seu nom, ja sigui perquè ell els va descobrir o per haver estat el primer a donar-hi una demostració completa i rigorosa. Tanmateix, si la seva aportació a la matemàtica és rellevant no és menys interessant el seu vessant humà i la seva contribució a la creació dels seminaris universitaris on es van originar gran part dels avenços científics del segle XX.

Els anys d’estudiant de Weierstrass

Karl Weierstrass va néixer el 31 d’octubre de 1815 a Ostenfelde, districte de Warendorf (Prússia, actualment Alemanya). El seu pare Wilhelm, membre d’una família d’artesans i petits comerciants des del segle XVI, home intel·ligent, format i que apreciava la bona educació, era llavors secretari de l’alcalde (Biermann, 1970-1990).

Quan tenia catorze anys, Karl Weierstrass va entrar a l’Institut Catòlic de Paderborn, on esdevingué un estudiant excel·lent, essent declarat «el millor de tots» en diverses matèries, entre les quals la matemàtica. És també en aquesta època que Karl treballà com a comptable, per ajudar a l’economia familiar, i que començà a llegir regularment la influent revista de matemàtiques Journal de Crelle: Journal für die Reine und Angewandte Mathematik (“Revista de matemàtiques pures i aplicades”).

Després de deixar l’institut, Karl Weierstrass va complaure el seu pare, que volia que estudiés finances públiques i administració, i va accedir a la Universitat de Bonn l’any 1834. Aquests estudis no el van motivar i després de vuit semestres sense aprovar res va tornar a casa dient que no volia estudiar aquesta carrera. No obstant això, a Bonn havia començat a llegir obres de matemàtiques, com ara el Traité de Mécanique celeste (1799-1825) de Pierre Simon Laplace (1749-1827), que el van impressionar. També va llegir l’obra de Carl Gustav Jakob Jacobi (1804-1851), Fundamenta nova theoriae functionum ellipticarum (1829), tot i que li va resultar massa complicada. Aleshores decidí llegir una obra anterior d’Adrien-Marie Legendre (1752-1833), Traité des fonctions elliptiques (1825), i apunts de les classes sobre funcions el·líptiques del que seria posteriorment el seu mestre, Christoff Gudermann (1798-1852).

Aquestes lectures, així com la carta de Niels Henrik Abel (1802-1829) a Legendre de l’any 1830 a la revista Journal de Crelle, el van decidir a estudiar matemàtiques. Weierstrass ho explica més tard, en una carta al matemàtic Marius Sophus Lie (1842-1899), el 10 d’abril de 1882:

Per mi, aquesta carta [d’Abel a Legendre], quan me’n vaig adonar a Crelle durant els meus anys d’estudiant, va ser de gran importància. La derivació immediata de la forma de representació de la funció donada per Abel, i designada per ell per λ(x), definint aquesta funció a partir de l’equació diferencial, va ser la primera tasca matemàtica que em vaig posar a mi mateix; i la seva afortunada solució em va decidir a dedicar-me totalment a les matemàtiques.

(Biermann, 1970-1990, pp. 219-220)

«L’any 1841 va escriure el seu primer article sobre la teoria de sèries de potències i la seva convergència»

Aquesta passió per les matemàtiques no l’abandonaria mai i encara que estudiava a la Universitat de Münster per a ser professor de secundària, l’any 1841 va escriure el seu primer article sobre la teoria de sèries de potències i la seva convergència. Christoff Gudermann, que li impartia classes sobre les funcions el·líptiques, reconeixent el seu talent, va insistir a dir-li que continués els seus estudis de matemàtiques i en el seu informe d’avaluació va escriure que Weierstrass era: «d’igual rang que els inventors que s’havien coronat amb glòria».

Karl Weierstrass esdevingué professor de secundària primer a Deutsch-Krone (1842-1848) i després a Braunsberg (1848-1855), tot i que l’any 1850 començà a trobar-se malament i a tenir atacs de vertigen que se li repetirien durant dotze anys. Foren anys durs d’investigació en solitari, sense biblioteques ni correspondència. Però aquestes recerques van donar els primers resultats. Així, l’any 1854 publicà l’article Zur Theorie der Abelschen Functionen (“Sobre la teoria de les funcions abelianes”), en què presentava una descripció del seu mètode per a la representació de les funcions abelianes per mitjà de les sèries de potències convergents. Quasi de seguida, el 31 de març de 1854, la Universitat de Königsberg li va conferir el grau de doctor honoris causa en reconeixement dels seus mèrits.

«Weierstrass es va dedicar durant tota la seva vida a fonamentar rigorosament una teoria completa i coherent de les funcions abelianes»

Dos anys més tard, Weierstrass publicà el famós article que aprofundeix en la teoria de les funcions abelianes: Theorie der Abelschen Functionen (“Teoria de les funcions abelianes”), on provà els resultats que en l’article anterior havia només descrit. Segons David Hilbert, Weierstrass havia obtingut un dels més grans resultats de l’anàlisi, la solució del problema de Jacobi sobre la inversió d’integrals hiperel·líptiques. De fet Weierstrass es va dedicar durant tota la seva vida a fonamentar rigorosament una teoria completa i coherent de les funcions abelianes.

Gràcies a aquestes contribucions, el 14 de juny de 1856 Weierstrass deixà l’institut de secundària i entrà al Berliner Gewerbeinstitut de la Technische Universität Berlin. Un any després va ser nomenat membre de l’Acadèmia de les Ciències de Berlín i passat un temps, el 1861, obtingué la plaça de professor a la Universitat de Berlín.

Weierstrass, a la Universitat de Berlín

L’any 1854, Karl Weierstrass publicà l’article Zur Theorie der Abelschen Functionen (“Sobre la teoria de les funcions abelianes”) al Journal de Crelle, on presentava una descripció del seu mètode per a la representació de les funcions abelianes per mitjà de les sèries de potències convergents (esquerra). Dos anys més tard, el 1856, Karl Weierstrass publicà al mateix Journal de Crelle el famós article que aprofundeix en la teoria de les funcions abelianes, Theorie der Abelschen Functionen (“Teoria de les funcions abelianes”), on provà els resultats que en l’article anterior havia només descrit (dreta). / Mètode

La Universitat de Berlín va ser creada l’any 1810, i del 1830 al 1840 ja havia accedit a una situació privilegiada amb Karl Gustav Jakob Jacobi, Peter Gustav Lejeune Dirichlet i Jakob Steiner. Però l’any 1851 va morir Jacobi, i el 1855 ho va fer Carl Friedrich Gauss, de manera que Dirichlet se’n va anar a la Universitat de Göttingen a substituir aquest últim. A Jacobi el va substituir Carl Wilhelm Borchardt (1817-1880), amic de Weierstrass i qui, des de l’any 1856 i fins el 1880, s’encarregà de la revista Journal de Crelle. A Dirich­let el va substituir Ernst Kummer (1810-1893). A aquests matemàtics s’hi va afegir Leopold Kronecker (1823-1891), alumne de Kummer i abans alumne de ­Dirichlet. Kummer va obtenir tan bona impressió de les contribucions de Weierstrass que li va aconseguir un lloc com a professor extraordinari a la Universitat de Berlín, on l’any 1864 va esdevenir catedràtic i, posteriorment, rector.

Kummer i Kronecker formaren amb Weierstrass el triumvirat que aconseguí que la Universitat de Berlín esdevingués un centre de gran prestigi per als estudis de matemàtiques. Des de l’any 1861 fins el 1886 van desenvolupar un pla biennal de cursos i cada dos anys repetien el mateix programa: «Introducció a la teoria de les funcions analítiques», «Teoria de les funcions el·líptiques», «Aplicacions de les funcions el·líptiques», «Teoria de les funcions abelianes», «Aplicacions de les funcions abelianes» i «Càlcul de variacions». Eren cursos molt reconeguts arreu d’Europa, hi assistien centenars d’alumnes cada any i alguns d’ells van esdevenir deixebles de Weierstrass. També hi assistien alumnes d’estudis postdoctorals. Així, Gösta Mittag-Leffler (1846-1927) explica que l’any 1873, quan va arribar a París a fer estudis postdoctorals amb Charles Hermite (1822-1901), les primeres paraules d’aquest van ser: «Vostè ha comès un error, senyor […]. Vostè hauria hagut de seguir els cursos de Weierstrass a Berlín. Ell és el nostre mestre» (Mittag-Leffer, 1902). I així ho va fer. L’any 1882, el mateix Weierstrass reconeixia que amb aquests cursos els estudiants tenien: «l’oportunitat de començar amb una sèrie de lliçons biennals a tractar la més important disciplina matemàtica en mesurada successió. Els temes que cobreixen són llegits poc o gens en altres universitats o no ho són amb regularitat» (Calinger, 1996, p. 166). Tanmateix, en aquesta època Weierstrass continuava patint problemes de salut, en aquest cas bronquitis i flebitis, i moltes vegades havia de fer les classes assegut.

Una altra de les aportacions valuoses de Weierstrass va ser la creació d’un seminari de matemàtiques a la Universitat de Berlín l’any 1860. Kummer i Weierstrass van presentar la sol·licitud al ministre de Cultura, Moritz von Bethmann-Hollweg, que incloïa dos objectius: primer, preparar millor els estudiants per ser professors, donant un coneixement més profund de les matemàtiques, i segon, donar-los experiència directa per obtenir de manera independent nous descobriments matemàtics.

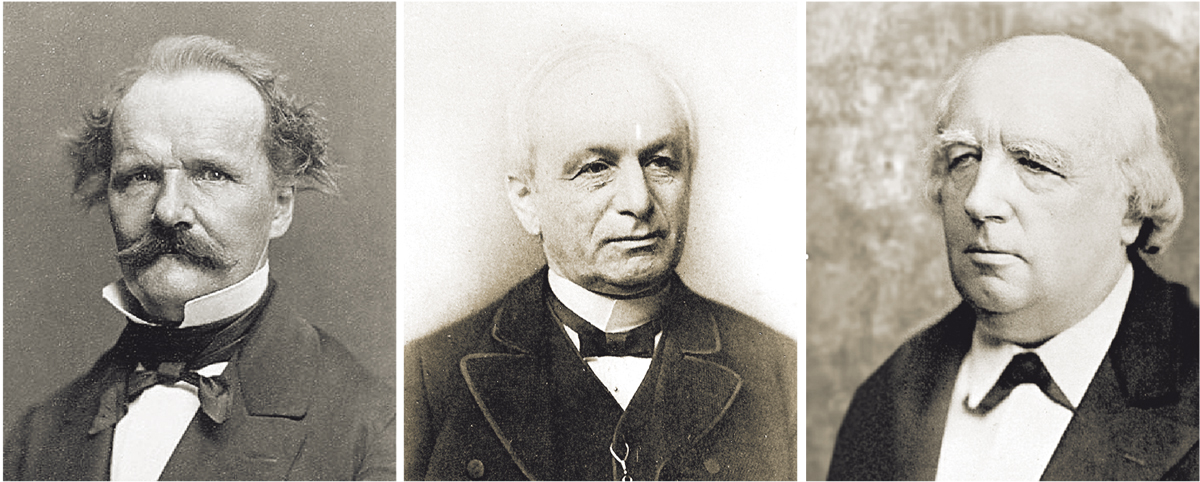
Kummer i Leopold Kronecker formaren amb Karl Weierstrass el triumvirat que aconseguí que la Universitat de Berlín esdevingués un centre de gran prestigi per als estudis de matemàtiques. / Mètode

El número vuit de la regulació del seminari de matemàtiques de la Universitat de Berlín descrivia que els seminaristes havien de participar en uns seminaris-tutories presentant una part de la seva recerca tant de manera oral com escrita. La part oral a vegades era una discussió oberta sobre la resolució de problemes matemàtics seleccionats proposats pels directors o bé pels mateixos seminaristes. Segons Weierstrass, només l’experiència de la recerca a generar nou coneixement podia il·luminar «els fonaments i la claredat» de les matemàtiques, la qual cosa era vital per excel·lir en l’ensenyament i l’aprenentatge de la disciplina.

La Universitat de Berlín va ser creada l’any 1810, i gairebé des del principi va comptar amb destacats matemàtics com Karl Gustav Jakob Jacobi, Peter Gustav Lejeune Dirichlet i Jakob Steiner. A la imatge, la Universitat de Berlín al segle XIX. / Mètode

En el seminari de matemàtiques, que va durar uns vint anys, el nombre de participants estava limitat a dotze per any i per entrar-hi havien de presentar un article o bé passar un examen. Els seminaristes tenien a la seva disposició una molt bona biblioteca (amb obres d’Abel, Cauchy, Euler, Monge i Poisson, entre d’altres), ja que la idea era treballar –sempre que fos possible– amb les fonts originals. També estaven subscrits a les revistes de matemàtiques més importants del segle XIX com ara Journal de Crelle, Journal de Liouville i Ar­chiv der Mathematik und Physik. També hi havia premis de recerca cada any. Així va ser com, a través d’aquest seminari de matemàtiques, els bons estudiants van ser reconeguts i ajudats. Entre els participants trobem nombroses figures rellevants com ara Ferdinand Georg Frobenius (1849-1917) i Wilhelm Killing (1847-1923).

Com que hi havia un nombre tan petit de seminaristes, Emil Lampe (1840-1918), Karl Hermann Amandus Schwarz (1843-1921) i d’altres van crear en paral·lel el novembre de 1861 un grup anomenat Unió Matemàtica, format per estudiants, que organitzava conferències, debats i que resolien problemes per millorar el coneixement matemàtic. La Unió, que va començar amb dotze membres i cap el 1880 ja en tenia uns vuitanta, va esdevenir un model per a altres universitats alemanyes. Weierstrass assistia també a les conferències i a les reunions de la Unió participant activament i debatent sobre els problemes matemàtics plantejats.

Les idees de Weierstrass sobre l’ensenyament-recerca de les matemàtiques, que es revelen totalment ac­tuals, van quedar ben reflectides en la seva conferència del 15 d’octubre del 1873, en ser nomenat rector de la Universitat de Berlín. Weierstrass assenyalava la importància de la selecció de materials i de l’èmfasi en els punts més rellevants en l’ensenyament dels professors universitaris:

L’èxit en la instrucció acadèmica depèn en gran mesura de la guia contínua del professor a l’alumne en algunes investigacions. Això, tanmateix, no es produeix només mitjançant la direcció pedagògica sinó principalment a través de la disposició dels materials i l’èmfasi, l’exposició de les lliçons del professor sobre la disciplina permet a l’alumne discernir les idees principals de manera apropiada. D’aquesta manera, el pensador plenament familiaritzat avança lògicament des de la madura i prèvia recerca i aconsegueix nous resultats o millors fonaments que els que existeixen.

(Weierstrass, 1894-1927, p. 335)

En aquesta conferència, Weierstrass explicava també que el professor ha de donar a conèixer els camins no reeixits o bé que s’intueixen, sense amagar-ne les dificultats o els errors comesos:

A continuació [el professor] no ha de deixar de determinar barreres encara no creuades per la ciència i assenyalar algunes posicions des de les quals seria possible un major progrés. Un [professor universitari] tampoc ha de negar a l’alumne una visió més profunda del progrés de les seves pròpies investigacions, ni ha de romandre en silenci sobre els seus propis errors del passat o [sobre les seves] decepcions.

(Weierstrass, 1894-1927, p. 336)

Els deixebles de Weierstrass, que es poden consultar en la pàgina web del Mathematics Genealogy Project, van ser nombrosos: 41 directes i 27.071 descendents. Algunes de les figures a qui Weierstrass va dirigir la tesi són molt conegudes. A tall d’exemple, es pot citar Leo Königsberger (1837-1921), Georg Cantor (1845-1918), Lazarus Fuchs (1833-1902), Sònia Kovalèvskaia (1850-1891) i Schwarz. Altres figures conegudes que van assistir als seus cursos van ser: Paul Bachmann (1837-1920), Felix Klein (1849-1925), Adolf Hurwitz (1859-1919), Mittag-Leffler i Sophus Lie, entre d’altres.

«Una deixebla singular va ser Sònia Kovalèvskaia, que als vint anys va anar des de Heidelberg a Berlín per estudiar matemàtiques amb Weierstrass»

Una deixebla singular va ser Sònia Kovalèvskaia, que als vint anys va anar des de Heidelberg a Berlín per estudiar matemàtiques amb Weierstrass. Aquest es va convèncer de seguida del talent de Sònia, tot i que, com que era una dona, no va aconseguir ser admesa al programa de doctorat de la Universitat de Berlín. Weierstrass li va donar classes particulars fins l’estiu de l’any 1874, quan va obtenir el doctorat a la Universitat de Göttingen. Aquest exemple ens mostra una vegada més la importància per a Weierstrass de fer avançar el coneixement salvant les dificultats que, en aquest cas, posava la societat. 

Weierstrass era molt estimat pels seus deixebles i el 31 d’octubre de 1885, quan va fer setanta anys, li van preparar una gran festa d’aniversari en què li van regalar una medalla commemorativa i un àlbum de fotos amb dedicatòries. A la festa hi van assistir 320 figures matemàtiques d’arreu d’Europa i totes es troben fotografiades en l’àlbum, moltes amb dedicatòries entranyables. El 1892 Weierstrass va ser premiat amb la medalla Helmholtz per l’Acadèmia de Ciències de Berlín i tres anys després, el 1895, amb la medalla Copley, el més alt guardó de la Royal Society de Londres. Aquell mateix any, amb motiu del seu vuitantè aniversari, se li va regalar també un retrat que va ser solemnement descobert a la Galeria Nacional de Berlín. Va passar els tres darrers anys de la seva vida en cadira de rodes, immòbil i dependent. Va morir a Berlín d’una pneumònia el 19 de febrer de 1897, quan tenia 82 anys.

«Cal assenyalar l’interès de Weierstrass perquè tot el que es publiqués derivat de les seves investigacions fos cert i rigorós»

Contribucions de Weierstrass

Encara que els cursos de Weierstrass foren publicats pels seus alumnes al llarg de la seva vida, veient que tot el seu llegat perillava a causa de les diferències amb Kronecker, va decidir editar ell mateix les seves obres completes. El 1894 va editar el primer volum, el segon, l’any 1895, i després de la seva mort els seus deixebles Johannes Knoblauch (1855-1915) i Georg Hettner (1854-1914) van editar fins a set volums, l’últim l’any 1927. Finalment, tots van ser reimpresos l’any 1967. Cal assenyalar l’interès de Weierstrass perquè tot el que es publiqués derivat de les seves investigacions fos cert i rigorós. Per a ell el més important no era l’autoria de la publicació, ni que ell fos citat, sinó que es pogués fer progressar veritablement el coneixement científic. Aquest vessant generós envers la recerca no era ni de bon tros habitual a l’època.

Segell commemoratiu que il·lustra el famós exemple de funció contínua no diferenciable a cap punt de Karl Weierstrass.

Pel que fa als seus articles, a tall d’exemple citarem el titulat «Remarques sur qualques points de la théorie des fonctions analítiques» (“Remarques sobre alguns punts de la teoria de funcions analítiques”) de l’any 1881. Weierstrass hi aclareix alguns punts sobre les seves idees de la teoria de funcions analítiques matisant la relació intuïtiva entre continuïtat i derivabilitat.

En la teoria de les funcions analítiques primer hi van treballar Abel i Jacobi. Més tard, Augustin Louis Cauchy (1789-1852) imposà que les funcions analítiques han de tenir una derivada contínua i Bernhard Riemann (1826-1866) donà a la imatge geomètrica un paper dominant i la funció, que cal representar, és la que transforma les figures. Weierstrass, en canvi, se situa en un punt de partida diferent: la sèrie de potències, «l’element de la funció» que està confinat en un cercle de convergència (Dugac, 1973; Poincaré, 1899). Així Weierstrass ja recorda que el seu camí és diferent de les vies ordinàries de desenvolupament de la teoria de funcions.

A les meves lliçons sobre els elements de la teoria de funcions, he posat en evidència, des del començament, dos teoremes que no s’acorden gens amb les vies ordinàries, a saber: I) Si una funció d’una variable real és contínua, no es pot pas concloure que, pels diversos valors de la variable, tingui una derivada determinada; encara menys es pot concloure que posseeix sempre una derivada contínua, almenys en uns intervals definits. II) Si una funció d’una variable complexa està definida per una certa regió d’aquesta última, no és pas sempre possible de continuar-la més enllà dels límits d’aquesta regió: en altres termes, existeixen funcions monògenes d’una variable que tenen aquesta propietat, que els punts del pla de la variable, pels quals no pot estar definida, no són pas solament punts aïllats, sinó que formen línies i superfícies.

(Weierstrass, 1881, pp. 178-179)

Weierstrass cita en aquest article el seu famós exemple de funció contínua no diferenciable a cap punt i aclareix també que la demostració concreta de la no derivabilitat l’havia envia­da per carta a Du Bois-Reymond i aquest l’havia publicada l’any 1875, tot i que Weierstrass ja l’havia presentada, el 18 de juny de 1872, a l’Acadèmia de Ciències de Berlín.

Dugac (1973) afirma que Weierstrass «rarament emprava la geo­metria i quan ho feia, ho feia només a títol d’il·lustració». També el seu estudiant Salvatore Pincherle (1853-1936), en el curs de Weierstrass que va publicar l’any 1880, assenyalava que, encara que intuïtivament sembli que tota funció contínua admet derivada, a vegades les representacions geomètriques enganyen els nostres ulls i aquest teorema es pot rebatre amb els exemples analítics de funcions no derivables a cap punt trobats en aquell temps. Tot seguit, Pincherle donava un altre exemple de funció contínua no derivable a cap punt:

Pincherle afegia, sense demostració ni representació, que aquesta funció és contínua i finita per a tots els valors reals de x de –∞ a +∞, i no té cap derivada (Pincherle, 1880, p. 71). L’exigència d’un mètode de demostració exclusivament aritmètic sense dependre de l’evidència geomètrica dins del model de rigor weierstrassià és el que va esdevenir la seva aritmetització de l’anàlisi matemàtica.

La investigació sobre l’obra de Weierstrass aporta, doncs, diversos elements de discussió sobre la comprensió de les idees matemàtiques: intuïcionisme o logicisme? En quins casos? Henri Poincaré (1899), quan comparava Riemann i Weierstrass, explicava que Riemann emprava com a instrument la intuïció, així ho veia tot d’un cop d’ull, com un viatger que mira des de dalt d’una muntanya. En canvi, Weierstrass prenia com a instrument l’anàlisi i feia veure tots els racons amb claredat. Llavors hom es pregunta, es comprèn millor una demostració fent totes les operacions elementals i detallades? No cal la intuïció? No cal la geometria? O calen els dos vessants per entendre les demostracions i avançar en el coneixement?

Altres preguntes que hom es pot fer referides més específicament al pensament matemàtic de Weierstrass són: La contribució de Weierstrass al desenvolupament de l’anàlisi matemàtica ha permès nous resultats? El límit, les derivades, la noció de veïnatge, tal com ho presenta Weierstrass, són determinants per avançar en el càlcul? Les paraules de David Hilbert sobre el significat d’aquestes contribu­cions, en l’homenatge a Weierstrass amb motiu dels cent anys del seu naixement, són de gran ajuda per reflexionar-hi:

Weierstrass, mitjançant una crítica conduïda amb magistral profunditat, va proveir a l’Anàlisi Matemàtica d’una base sòlida. En dilucidar entre d’altres sobre les nocions de mínim, de funció, de derivada, ha eliminat les objeccions que encara suscitava el càlcul infinitesimal, netejant-lo de totes les idees confuses sobre allò infinitament gran i allò infinitament petit i ha superat definitivament les dificultats que provenen de les nocions mateixes d’infinitament gran i d’infinitament petit.

(Hilbert, 1926, p. 91)