The Strange Attraction of Chaos. Dissipative dynamical systems continuously lose energy and this fact determines their final fate within the space where they exist. So-called “strange attractors” are particularly interesting when considering their possible end. The author discusses their origin and the reasons why they are so complex.
Introducció
Suposem que tenim cert fenomen (físic, químic, biològic, econòmic, etc.), del qual ens interessa conèixer l’evolució de certes variables dependents del temps. Exemples típics poden ser el moviment de partícules sotmeses a la força de gravetat, on les variables serien les posicions i velocitats de cadascuna de les partícules, o l’evolució d’una població, on la variable seria el nombre d’individus. En molts casos es poden trobar models matemàtics que ens permeten conèixer l’evolució de les variables de forma aproximada. Els models més simples consisteixen en equacions diferencials ordinàries, quan considerem el temps continu o equacions en diferències (també anomenats sistemes dinàmics discrets), quan el considerem discret. Donat un estat inicial de les variables, la resolució de l’equació diferencial ens permet obtenir el seu valor en qualsevol temps posterior. Una equació en diferències consisteix en una transformació (aplicació) que, donat un valor inicial de les variables, permet obtenir el valor de les variables al cap d’un cert temps (primer iterat), de dues vegades aquest temps (segon iterat), i així successivament. Els dos casos esmentats reben també el nom de sistemes deterministes.
«L’estat de l’atmosfera no es pot predir de manera fiable a llarg termini, perquè el seu comportament és caòtic»
Els models esmentats també dependran sovint de certs paràmetres que ens interessarà variar, tant sigui per descriure els diferents comportaments possibles de les solucions, com per trobar els valors que s’ajusten millor al nostre problema original. Una vegada hem obtingut un bon model, el següent pas és estudiar quin és el comportament de les variables dependents respecte el temps. Aquest és l’objectiu de la teoria general dels sistemes dinàmics. Arribats aquí hom pot pensar que el comportament ha d’ésser simple, ja que és completament determinista: coneguda la condició inicial, podem saber sense cap mena de dubtes quina serà la condició final al cap d’un cert temps. Tanmateix, si el model no és excessivament simple, pot succeir que una petita variació en les condicions inicials doni lloc a una gran variació en les condicions finals. Aquest és el fenomen que s’anomena dependència sensible a les condicions inicials. Com que, en la pràctica, el valor inicial de les variables no es pot conèixer exactament, i a més els càlculs de les òrbites només es poden fer amb una precisió limitada, això fa que no sigui possible donar valors fiables de les variables al cap d’un temps més o menys llarg. Tenim, doncs, una aparent paradoxa: un sistema determinista es pot comportar com si fos aleatori. Aquest comportament és el que sol rebre el nom de caos determinista. En aquest moment sorgeix la següent pregunta: si un sistema és caòtic, com es pot conèixer el comportament de les seves òrbites? La resposta és que per a un període de temps curt això no serà problema, però sí per a un temps llarg. En aquest article ens interessarem per un tipus de comportament caòtic que apareix per sistemes dissipatius, és a dir, sistemes que perden energia a mesura que augmenta el temps. En aquest cas, poden aparèixer els anomenats atractors estranys, que són conjunts en l’espai de variables del sistema, molt complexes geomètricament, i tals que per a qualsevol condició inicial, la solució corresponent es va acostant cada vegada més, a mesura que augmenta el temps, cap a aquest conjunt, però sense acostar-se a cap punt concret d’aquest conjunt. És a dir, quan el temps sigui prou gran, podem suposar que la solució es mou, de manera aparentment impredictible, sobre l’esmentat conjunt.
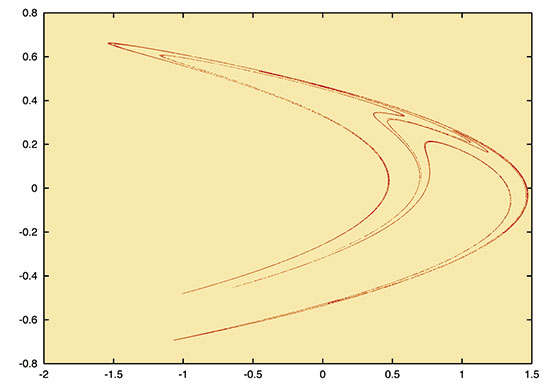
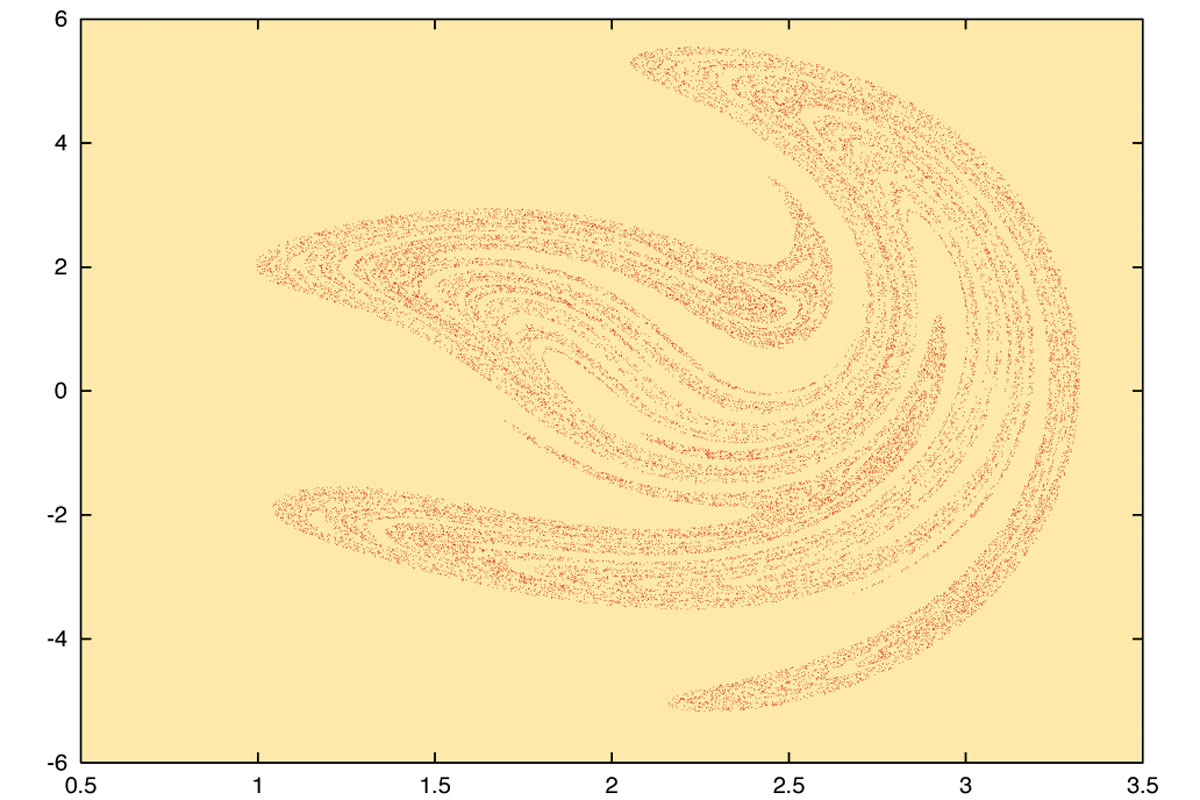
Figura 2: Atractor estrany per l’aplicació d’Hénon, amb a=1.15, b=0.45
Un cas especialment paradigmàtic és el de l’estudi de l’evolució de l’estat de l’atmosfera terrestre, que ens hauria de permetre fer prediccions del temps. Com és conegut, l’estat de l’atmosfera no es pot predir de manera fiable a llarg termini. Això és degut no solament al fet que els models utilitzats poden no ésser suficientment acurats, sinó també al fet que el comportament de la atmosfera terrestre és caòtic, en el sentit que hem donat anteriorment.
A les figures 1 i 2 tenim dos exemples típics d’atractors estranys, corresponents, respectivament, a una equació diferencial, que anomenarem equació de Duffing forçada, i a un sistema dinàmic discret, que anomenarem aplicació d’Hénon. L’equació de Duffing modela molts problemes que involucren oscil·ladors no lineals amb esmortiment i forçament. Per dibuixar l’atractor, primer hem de definir un sistema discret associat anomenat aplicació de Poincaré. Per als lectors interessats, hem posat la fórmula, els paràmetres usats, i hem indicat la manera de construir l’aplicació de Poincaré, a la mateixa figura. L’aplicació d’Hénon es pot definir com una transformació que a cada punt en el pla (x,y) fa correspondre el punt (1+y-ax²,bx). La manera d’obtenir aquests dibuixos és la següent: Agafem una condició inicial qualsevol en el rectangle dibuixat i calculem els primers 100 iterats i dibuixem els 30.000 següents. El dibuix que surt és l’atractor estrany i no depèn de la condició inicial escollida.
A continuació, veurem per què els atractors estranys apareixen i tenen una estructura geomètrica complexa. Per això haurem d’introduir certs objectes bàsics de la teoria de sistemes dinàmics, com són les òrbites periòdiques i les varietats invariants. Per acabar aquesta introducció voldríem remarcar la importància de saber que un sistema té un atractor estrany, i la seva situació en l’espai de variables del sistema. Si pensem novament en la predicció del temps, i suposem que coneixem aquest atractor estrany, podem assumir que les variables del sistema en aquest moment, o qualsevol d’altre posterior, es troben situades sobre l’atractor. Per tant, donades unes condicions inicials aproximades, les podrem ajustar perquè estiguin sobre l’atractor estrany, i això ens donarà una predicció més acurada del temps. Cal dir, d’altra banda, que, en qualsevol cas, això no ens permetrà fer una bona predicció a llarg termini.
«Els atractors estranys tenen una estructura geomètrica complexa»
Punts periòdics, varietats invariants i atractors estranys
Suposem que volem estudiar un sistema dinàmic discret. El primer que cal fer és trobar els objectes invariants que apareixen. Els més simples són les òrbites periòdiques. Una òrbita periòdica és una solució que al cap d’un cert temps discret (o nombre d’iterats de l’aplicació) torna a donar els valors que tenia inicialment. S’anomena punt fix si el període és igual a 1. Si el model representa un sistema dissipatiu, hi ha altres objectes invariants interessants anomenants atractors. Com el seu nom indica, un atractor és un conjunt de valors de les variables dependents, que tenen la següent propietat: donada una condició inicial no massa lluny de l’atractor, la distància entre la solució corresponent i l’atractor tendeix a zero quan el temps tendeix a infinit. Per tant, la major part del temps la solució estarà molt a prop d’algun dels elements d’aquest conjunt. El cas més simple és quan aquest conjunt és un punt fix. En tal cas sabem que donada qualsevol condició inicial prou propera a l’atractor, al cap d’un temps més o menys llarg la solució serà pràcticament constant. Un exemple molt simple d’aquesta situació és considerar un pèndol amb fregament. Si deixem anar el pèndol a una certa alçada, al cap d’unes quantes unitats de temps semblarà estar parat en la posició més baixa possible (equilibri estable).
Una anàlisi acurada dels dos exemples esmentats en la introducció ens demostra que tant l’aplicació de Poincaré del sistema de Duffing com l’aplicació d’Hénon tenen punts fixos i periòdics, que, com veurem, representen un paper essencial en la comprensió dels atractors estranys.
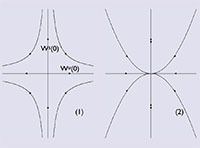
Figura 3: Comportament d’una aplicació prop d’una sella (1) i d’un node (2).
Ara voldríem saber com es comporta un sistema dinàmic discret prop d’un punt fix. Si l’espai en què estan definides les variables dependents té dimensió 2, es pot demostrar que quasi tot punt fix ha d’ésser d’un dels dos tipus següents: sella o atractor. En la figura 3 hem dibuixat un esquema simplificat del comportament de les òrbites d’una aplicació prop d’un punt fix sella (1) i prop d’un tipus d’atractor anomenat node (2). Amb això volem dir que en un cas real el comportament de les òrbites seria similar, però les línies que apareixen estarien deformades.
La interpretació dels dibuixos és la següent: tant en (1) com en (2) la intersecció de les dues rectes perpendiculars és el punt fix. Si considerem un punt en les línies dibuixades la seva imatge estarà en la mateixa línia. Les fletxes indiquen cap a on es dirigeixen les imatges dels punts de la línia. En el cas de la sella tenim que el comportament d’una òrbita qualsevol és el següent: els iterats en principi s’acosten al punt fix fins que arriben a una distància mínima i després s’allunyen. Només hi ha dues excepcions a aquest comportament: si la condició inicial està sobre la recta vertical, llavors els iterats corresponents tendeixen al punt fix, i si està sobre la recta horitzontal els iterats temps enrere també tendeixen al punt fix. Hem usat per a aquestes dues rectes la notació Ws, que correspon al que s’anomena varietat invariant estable, i Wu, que correspon a l’anomenada varietat invariant inestable. En (2) el que observem és que, per a qualsevol condició inicial, els successius iterats tendeixen al punt fix. En aquest últim cas, les dues fletxes en la recta vertical indiquen que l’atracció és més forta en aquesta direcció.

Figura 4: Varietats invariants d’un punt fix sella amb interseccions homoclíniques.
Les varietats invariants d’un punt fix sella tenen propietats notables. Per simplificar continuarem suposant que la dimensió de l’espai de les variables dependents és 2. Esmentem-ne algunes: Ws i Wu són corbes suaus de longitud infinita i invariants. Varietats estables no es poden tallar amb varietats estables, ni varietats inestables es poden tallar amb varietats inestables. En particular una varietat invariant estable o inestable no pot tenir interseccions amb si mateixa. Un punt d’intersecció d’una varietat estable Ws(p) d’un punt fix p amb una varietat inestable Wu(q) d’un punt fix q s’anomena punt homoclínic si p=qheteroclínic si p≠q. A causa de la invariància de Wu i Ws, si un punt és homoclínic (resp. heteroclínic), tota l’òrbita que té aquest punt com a condició inicial està formada per punts homoclínics (respectivament heteroclínics) i per tant se l’anomena òrbita homoclínica (resp. heteroclínica). L’estructura de les varietat invariants estable i inestable és força complexa quan existeixen òrbites homoclíniques o heteroclíniques, com es pot veure a la figura 4. En aquesta mateixa figura, observem que, tal com hem dit, prop del punt fix sella (representat per un petit quadrat) el comportament de les òrbites és similar al que hem descrit abans, però no lluny del punt fix.
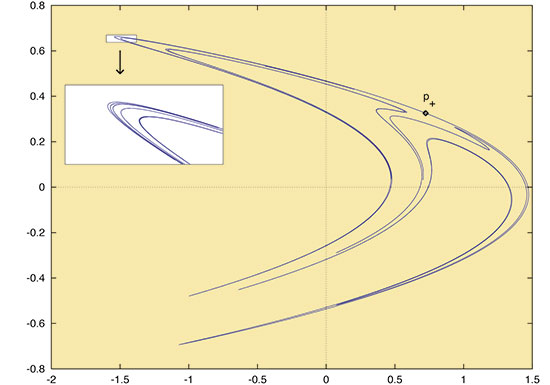
Figura 5: Varietat invariant inestable del punt fix p+, per a a=1.15 i b=0.45, que presumiblement forma part d’un atractor estrany. En la part superior esquerra hi ha una ampliació d’un petit rectangle tal com indica la fletxa.
En els dos exemples que hem donat, es pot demostrar que existeixen punts fixos de tipus sella dins de l’atractor estrany amb interseccions homoclíniques. Llavors, la varietat invariant inestable del punt fix està continguda en l’atractor estrany i forma el que podríem dir el seu “esquelet”. En les figures 5 i 6, respectivament, hem dibuixat les varietats invariants inestables de l’aplicació d’Hénon i de l’equació de Duffing. Si comparem aquestes figures amb els atractors estranys corresponents (figures 2 i 1 respectivament), veiem que són molt similars. Cal remarcar que no podem dibuixar tota la varietat invariant (ja que té longitud infinita) i és per això que els dibuixos no encaixen exactament. En la figura 5 hem dibuixat també una ampliació d’una part de la varietat. Aparentment, està formada per infinites corbes de tipus parabòlic. Una propietat interessant és que la distribució d’aquestes corbes no és uniforme, però si fem més ampliacions veuríem essencialment el mateix tipus de comportament. Podem dir, doncs, que la varietat invariant és autosimilar si canvia l’escala, o, dit d’una altra manera, que té estructura fractal.

Figura 6: Varietat invariant inestable d’un punt fix de l’atractor estrany de l’equació de Duffing, per a k=0.02 i b=6.8.
Finalment, els sistemes que hem esmentat depenen de paràmetres. En variar aquests paràmetres els atractors estranys desapareixen i es converteixen en òrbites periòdiques atractores o en atractors estranys més petits formats per diverses peces. Tanmateix, podem veure que hi ha molts valors dels paràmetres per als quals existeixen atractors estranys, encara que variacions molt petites d’aquests valors poden fer canviar de manera dramàtica el comportament del sistema.
En conclusió, tant l’existència d’atractors estranys, com la seva complexitat, són degudes a l’existència de varietats invariants amb interseccions homoclíniques. Per tant, l’estudi d’aquestes varietats és la clau que ens permet entendre el comportament de les òrbites d’un sistema a llarg termini.





