Què entenem per diversitat?

El concepte de diversitat biològica ha evolucionat des del mer recompte d’espècies a càlculs més sofisticats que tenen en compte les abundàncies relatives i fins i tot el temps de divergència evolutiva entre espècies. En el curs d’aquesta evolució, les formes de mesurar la diversitat ben sovint s’han manllevat d’altres disciplines. El raonament evolutiu sobre la diversitat sol assumir implícitament que els càlculs de diversitat responen a certes propietats matemàtiques, però la majoria de càlculs tradicionals que realitzaven els biòlegs no complien aquestes propietats, una situació que sovint conduïa a inferències invàlides en termes matemàtics i biològics. Ara els biòlegs solen transformar els càlculs tradicionals en el «nombre efectiu d’espècies», la base matemàtica del qual s’adapta a la majoria de regles d’inferència que apliquen els biòlegs. El nombre efectiu d’espècies, per tant, sembla reflectir la majoria (no tot) del que els biòlegs entenen per diversitat.

Paraules clau: diversitat, nombre efectiu d’espècies, entropia de Shannon, riquesa d’espècies.

«A pesar de la seua importància, en biologia no hi ha un consens sobre el que significa en  realitat la diversitat»

Diversitat és alhora una paraula de moda i un concepte científic precís que podem trobar en moltes disciplines. És un dels conceptes fonamentals de la biologia, particularment de les subdisciplines de l’ecologia, la teoria evolutiva i la genètica, però el mateix concepte –o un anàleg pròxim– representa un paper important en l’economia, la teoria de la informació i la física, entre altres camps. No obstant això, a pesar de la seua importància, en biologia no hi ha un consens sobre el que significa en realitat o com hauríem de quantificar-la. Aquesta mena de problema sempre és enrevessat per a una cièn­cia jove. Podríem aconseguir un significat més precís simplement definint la diversitat d’una manera determinada, però això és una solució simplista; no hi ha res que ens garantesca que la diversitat, definida en aquests termes, connecte de manera significativa amb futures teories. En compte d’establir una definició forçada de diversitat, la biologia ha evolucionat gradualment cap a un concepte de diversitat que cada vegada respon a més requisits teòrics i pràctics nous.

«En la pràctica, comptar amb precisió el nombre d’espècies presents en comunitats riques resulta quasi impossible»

Primers càlculs de la biodiversitat

Quan els biòlegs van començar a parlar de diversitat només es referien al nombre d’espècies en una comunitat, el que es coneix com a «riquesa d’espècies». A primera vista, aquest concepte de diversitat sembla senzill d’interpretar, i sens dubte reflecteix una qualitat important d’un ecosistema. En la pràctica, però, comptar amb precisió el nombre d’espècies presents en comunitats riques, en què la majoria d’espècies solen ser rares, es fa quasi impossible. Per exemple, Phil DeVries, Tom Walla i Harold Greeney van recopilar papallones durant deu anys en una única localització de la selva amazònica (DeVries i Walla, 2001). I després d’aquells deu anys d’intensa recol·lecció hi continuaven afegint espècies que mai abans havien arreplegat. Això és típic dels ecosistemes tropicals. En llocs com aquests, el recompte d’espècies depèn en gran manera del treball de mostreig i de la distribució d’abundància de les seues espècies. Utilitzant eines estadístiques basades en els descodificadors que Alan Turing va crear per als britànics durant la Segona Guerra Mundial, Anne Chao va desenvolupar un estimador del límit inferior del nombre d’espècies d’una comunitat (Chao, 1984), però és impossible estimar sense biaixos el nombre real d’espècies.

A pesar de la dificultat d’estimació, la riquesa d’espècies continua sent un paràmetre de la comunitat bio­lògica important per a molts propòsits teòrics i pràctics. Per exemple, és molt útil per a prioritzar àrees de conservació. No obstant això, per a moltes aplicacions, no hi ha prou amb el mer recompte d’espècies. Una roureda amb alguns pins és molt diferent d’una pineda amb alguns roures. En molts aspectes ecològics, una comunitat de papallones amb deu espècies que incloga una espècie abundant i nou d’extremadament rares s’assembla més a una comunitat de papallones amb una única espècie que a una amb deu espècies igual de comunes. La forma com es distribueixen els individus de les espècies és important. Un recompte que només tinga en compte la presència o absència d’espècies no reflecteix aquesta diferència. Els biòlegs necessitaven expandir el concepte de diversitat per a tenir en compte l’abundància sempre que siga necesari. Per a un nombre determinat d’espècies, la major diversitat possible es donaria quan totes les espècies són igual de comunes, i el mínim possible quan totes les espècies menys una són extremadament rares. En aquest cas, la diversitat continuaria disminuint segons s’anaren extingint espècies.

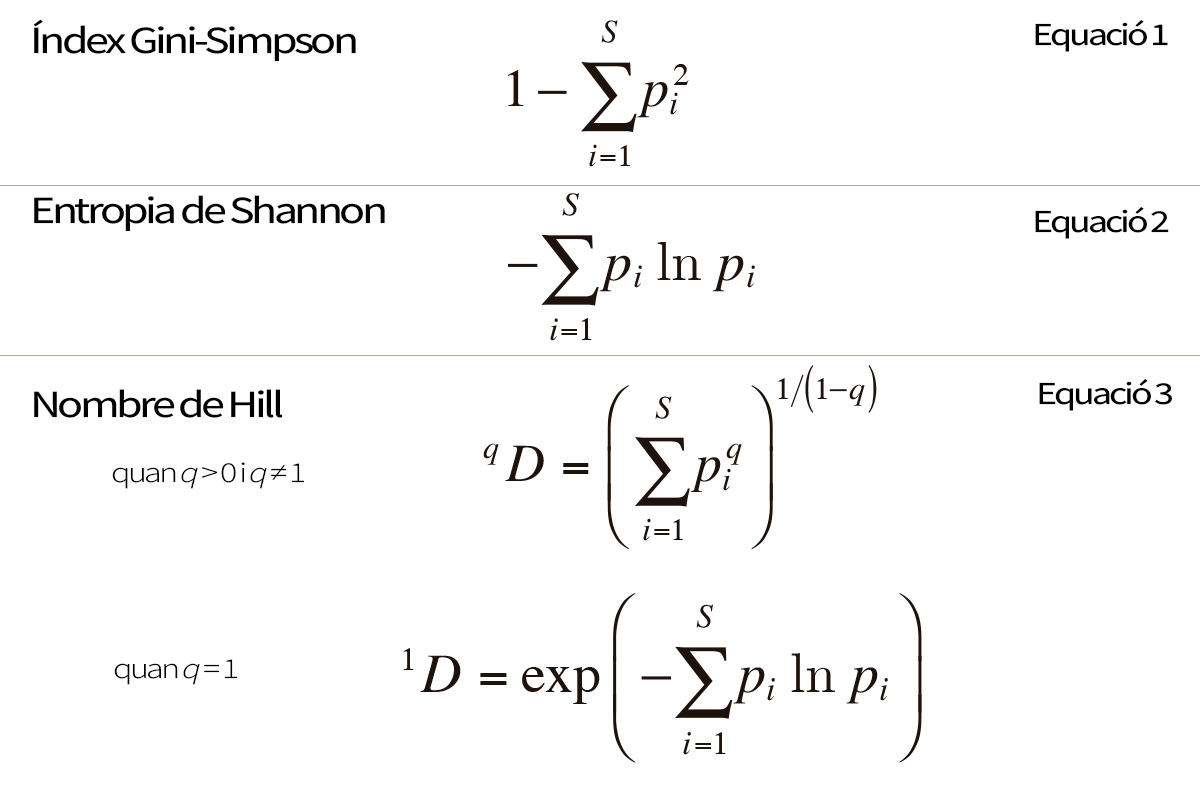
Taula 1. Les expressions matemàtiques més importants utilitzades per al càlcul de la diversitat ecològica. S = nombre d’espècies; pi = abundància relativa de l’espècie i (el nombre d’individus de l’espècie i en la comunitat dividit pel nombre total d’individus de totes les espècies, S); q és un paràmetre que determina la sensibilitat de la fórmula a les abundàncies relatives de les espècies.

Els càlculs d’aquest tipus són importants en moltes disciplines que s’ocupen de sistemes complexos. Són especialment prominents en economia, on s’utilitzen (aquests o altres càlculs inversos o complementaris) per a calcular coses com la concentració de la riquesa entre individus o la concentració de capacitat indus­trial entre corporacions. Ja fa temps que els economistes van formalitzar les condicions necessàries perquè disminuesca la concentració (i augmente el seu invers, la diversitat). La condició principal es coneix com a «principi de transferències Pigou-Dalton» (Jost, 2010). Expressat en termes biològics, per a un nombre fix d’espècies i un nombre fix d’individus, la diversitat hauria d’augmentar quan es transfereix abundància des d’una espècie a una altra més rara. La diversitat també augmentaria quan s’afegeix una espècie extremadament rara.

Moltes propietats d’un ecosistema importants en termes biològics obeeixen al principi de transferència. Per exemple, imaginem un ecosistema amb un nombre determinat d’espècies en què cada individu deambula a l’atzar i ocasionalment es troba amb un altre individu. Quan dos individus es troben, es pot calcular la probabilitat que els dos pertanguen a espècies distintes. Això es coneix habitualment com a índex Gini-Simpson (Equació 1 de la Taula 1), i en el passat s’entenia sovint com un equivalent de la diversitat. La probabilitat d’una trobada entre espècies és mínima quan totes les espècies menys una són extremadament rares. En transferir abundància des de les espècies més comunes a les més rares, la probabilitat augmenta fins que assoleix un màxim quan totes les espècies són igual de comunes. Per tant, la «probabilitat d’una trobada entre espècies» obeeix al principi de transferència i pot servir com a mesura de la complexitat compositiva d’un ecosistema. Una altra propietat d’un ecosistema d’aquest tipus és la incertesa sobre l’espècie d’un individu de la comunitat seleccionat a l’atzar. Aquesta incertesa es pot calcular a partir de les abundàncies relatives de cada espècie mitjançant la teoria de la informació (Shannon, 1948), i és simplement l’entropia de Shannon (Equació 2 de la Taula 1). Els biòlegs solen denominar-lo índex de Shannon-Weiner o índex de Shannon-Weaver. Per a un nombre donat d’espècies, aquest índex assoleix el mínim quan totes les espècies menys una són extremadament rares, i el màxim quan totes les espècies són igual de comunes. En el passat, aquesta mesura de la complexitat compositiva també es va equiparar amb la diversitat.

Interpretar els càlculs de diversitat

Els tres càlculs mencionats fins ara –la riquesa d’espècies, l’entropia de Shannon i l’índex Gini-Simpson– s’han utilitzat per a quantificar la diversitat, sovint al mateix temps. No obstant això, cadascun d’ells s’expressa en unitats distintes i presenta comportaments matemàtics diferents. La riquesa d’espècies és una mesura discreta amb valors sencers, expressada en «espècies», mentre que l’entropia de Shannon és una funció contínua sense límit superior, expressada en «bits», i l’índex Gini-Simpson és una probabilitat que mai pot excedir la unitat. Encara que sens dubte aquests càlculs estan relacionats amb el concepte biològic de diversitat, tenen propietats matemàtiques tan diferents que els seus valors no es poden comparar directament i, en general, la lògica que funciona amb un d’aquests és invàlida quan s’aplica als altres dos. Aquest caos pareixia impedir que els experts aconseguiren un concepte de diversitat rao­nablement precís però també general i profitós.

«La riquesa d’espècies continua sent un paràmetre de la comunitat biològica important per a molts propòsits teòrics i pràctics»

No obstant això, els biòlegs continuaven aplicant rao­naments semblants als tres càlculs, com si tingueren un únic concepte de diversitat en ment. Per exemple, habitualment s’analitzava el canvi percentual de cadascun d’aquests càlculs després d’un impacte humà o natural. Això era problemàtic perquè els biòlegs comparaven percentatges o proporcions amb càlculs clarament no lineals (Moreno, Barragán, Pineda i Pavón, 2011). Aquest mètode per a jutjar la magnitud d’un impacte podia oferir resultats enganyosos quan s’aplicava a l’entropia de Shannon, una mesura logarítmica. Era encara més enganyós quan s’aplicava a l’índex Gini-Simpson. Com que en aquest índex no pot excedir la unitat, totes les comunitats amb alta diversitat tenen valors semblants, molt pròxims a la unitat. Un canvi biològic enorme en una comunitat (per exemple, l’extinció d’un 90 % de les espècies) podria provocar un canvi inferior a un 1 % en el valor d’aquest índex.

Aquest problema es va fer més obvi quan els biòlegs van començar a utilitzar aquests càlculs de la diversitat per avaluar la similitud compositiva entre comunitats. Els biòlegs van notar que hi havia una connexió molt profunda entre similitud compositiva i diversitat. Si s’agrupen en la mateixa proporció dues comunitats que tenen les mateixes espècies amb la mateixa abundància relativa, la diversitat de la comunitat agregada serà la mateixa que la de les comunitats originals. D’altra banda, si la composició de les dues comunitats era molt diferent, llavors la diversitat de la comunitat agregada serà molt major que la mitjana de diversitat de les dues comunitats individuals. Comparant la diversitat mitjana de cada comunitat amb la diversitat de la comunitat agregada, es podria quantificar el grau relatiu de similitud compositiva entre elles. Normalment es comparava dividint les dues diversitats (Lande, 1996). Això era útil quan la mesura de la diversitat utilitzada era la riquesa d’espècies, però per a l’entropia de Shannon i l’índex Gini-Simpson, presentava el mateix problema mencionat en el paràgraf anterior: aquests càlculs són no lineals, per la qual cosa comparar les proporcions és enganyós. Per exemple, l’índex Gini-Simpson no pot excedir d’1,00, per la qual cosa, quan els índexs Gini-Simpson de les comunitats individuals s’acosten a la unitat, agregar-los-hi no fa que l’índex augmente molt, fins i tot quan les comunitats són completament diferents (sense espècies en comú). En dividir aquestes dues diversitats necessària­ment obtenim un nombre pròxim a la unitat, la qual cosa en teoria apunta a un alt nivell de similitud composicional, sense importar si les comunitats són quasi idèntiques o completament distintes (Jost, 2006, 2007; Jost et al., 2010).

La dificultat d’interpretar aquest i altres resultats de l’índex Gini-Simpson i l’entropia de Shannon va portar alguns biòlegs a dubtar de la utilitat d’aquests càlculs en biologia. El problema, però, no eren els càlculs sinó la insistència dels biòlegs a aplicar les mateixes regles d’inferència a tots, com si tots tingueren les mateixes propietats matemàtiques que la riquesa d’espècies.

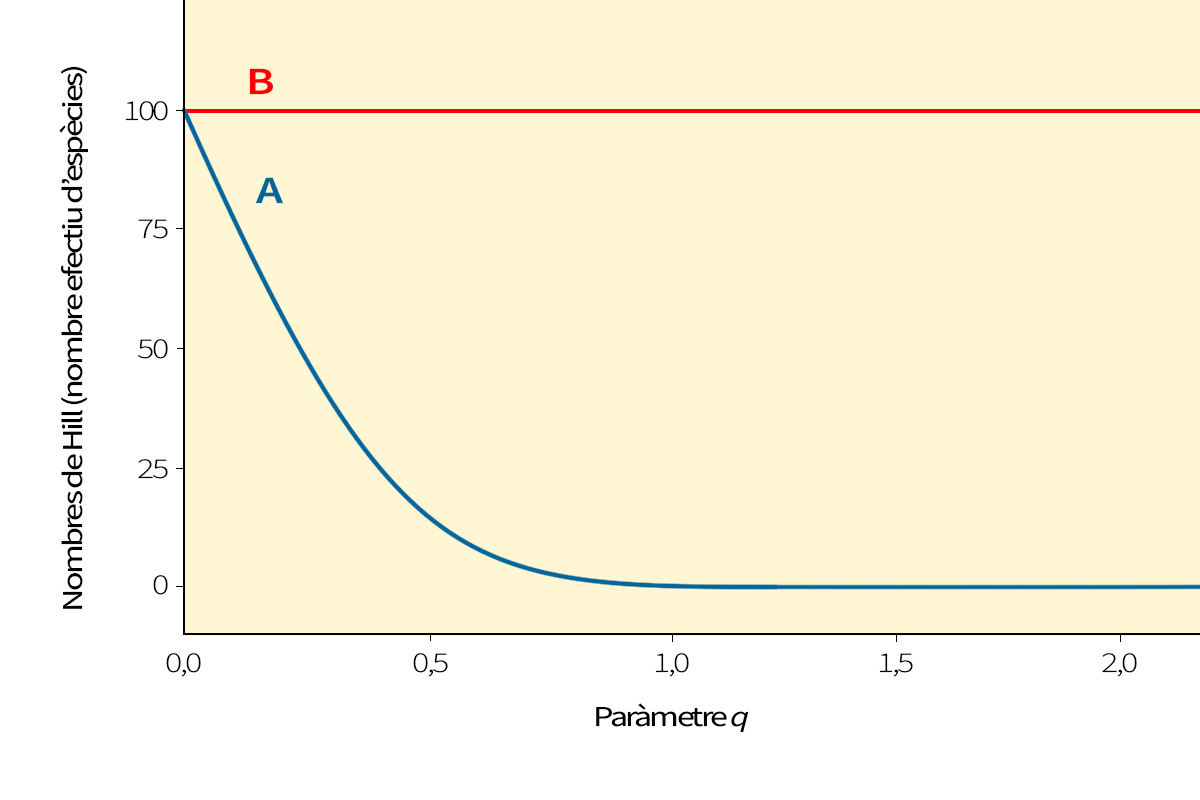
Figura 1. Perfils de diversitat de dues comunitats amb el mateix nombre d’espècies (s = 100) i individus (n = 1.000), però amb diferent equitativitat. En el perfil A, hi algunes poques espècies que són molt dominants, mentre que altres són poc abundants. En el perfil B, totes les espècies tenen un nombre semblant d’individus; és a dir, hi ha major equitativitat. Les xifres de Hill (el nombre efectiu d’espècies) fan de fórmula mestra que permet expressar de manera senzilla aquest nombre efectiu d’espècies enfront del paràmetre q, que determina la sensibilitat del càlcul a l’abundància relativa d’espècies. Això ens permet comparar, també gràficament, diversos perfils de diversitat com A i B. Ambdues comunitats tenen el mateix nombre d’espècies, per tant la mateixa diversitat d’ordre q=0, però el repartiment dels individus entre espècies és diferent: un desequilibri més gran (menor equitativitat) es tradueix en una menor diversitat d’ordre 1 i d’ordre 2 per a la comunitat A.

Cap a una fórmula mestra

Un pas clau va ser el descobriment –realitzat independentment a final del segle xx per científics de camps tan diferents com l’ecologia, l’economia, la teoria de la informació i la física– que aquests tres càlculs de la «diversitat» aparentment no relacionats (o les seues transformacions simples) podien, de fet, estar generats per una única fórmula mestra. Es van descobrir diverses fórmules mestres, diferents en cada disciplina, però només hi havia petites transformacions entre unes i altres, per la qual cosa expressaven essencialment el mateix. La majoria es van interpretar com a generalitzacions de l’entropia de Shannon. Una de les més conegudes d’aquestes fórmules mestres va generar la família d’entropies de Rényi (Rényi, 1961), i una altra molt popular va donar lloc a les entropies de Tsallis (o HCDT)¹ (Tsallis, 1988). Aquestes fórmules mestres poden generar cadascun dels tres càlculs de «diversitat» (o transformacions simples d’aquests) variant un paràmetre q que controla la sensibilitat del càlcul a les abundàncies relatives de les espècies. Quan q = 0, cadascuna d’aquestes fórmules mestres proporciona la riquesa d’espècies, o una transformació simple d’aquesta; quan q = 1, les fórmules mestres no estan definides, però en el límit pròxim a 1 proporcionen l’entropia de Shannon, o una transformació simple d’aquesta; i quan q = 2, les fórmules mestres proporcionen l’índex Gini-Simpson, o una transformació simple d’aquest. Això representava una unificació interessant i important del que anteriorment pareixia un garbull de càlculs sense relació entre ells. Era el primer senyal que podia existir una «matemàtica de la diversitat» rica i profunda per a posar ordre en la disciplina.

Aquestes fórmules mestres no es limiten als valors 0, 1 o 2 per al paràmetre q. Es podria usar qualsevol valor de q ≥ 0, i, en fer la gràfica de la fórmula mestra amb q, es podria crear una corba suau anomenada «espectre d’entropia (de Rényi o de Tsallis)» de la comunitat. Aquestes corbes ens ofereixen una forma alternativa d’expressar la informació continguda en la distribució d’abundàncies per espècie en una comunitat. Si comparem dues comunitats i observem quin perfil queda per damunt, no hi ha dubte de quina és més diversa. Si els perfils s’encreuen, l’ordre de diversitat és ambigu i depèn de la ponderació de les abundàncies relatives d’espècies.

El següent gran pas va ser el descobriment realitzat per l’ecòleg Mark Hill i els economistes Hannah i Kay que les fórmules mestres es podien transformar per a generar un grup de càlculs (Equació 3 de la Taula 1) amb la mateixa mètrica senzilla de la riquesa d’espècies, en compte d’entropies no lineals (Hannah i Kay, 1977; Hill, 1973). Els càlculs generats per la nova fórmula mestra obeeixen a un principi que ja era clau en l’economia moderna, i que estava implícit en molts dels raonaments dels biòlegs respecte a la diversitat. En economia es coneixia aquest principi com a «principi de replicació»: si agreguem una quantitat N de comunitats igualment diverses i de la mateixa grandària però que no comparteixen espècies, la diversitat de la comunitat agregada hauria de ser N vegades la diversitat d’una sola de les comunitats. Els càlculs que obeeixen a aquest principi són lineals pel que fa a l’agregat. Heus ací la solució al mal costum de comparar percentatges amb l’entropia de Shannon o l’índex Gini-Simpson! Ara aquests dos càlculs i d’altres de relacionats per a diferents valors del paràmetre q es podien transformar en càlculs que oferiren els resultats correctes en comparar proporcions i percentatges. Finalment vam aconseguir càlculs de la diversitat que abonaven les regles d’inferència que els biòlegs havien utilitzat prèviament en càlculs no lineals inadequats.

«Una roureda amb alguns pins és molt diferent d’una pineda amb alguns roures. La forma en què es distribueixen els individus de les espècies és important»

Aquests nous càlculs de la diversitat s’expressen en unitats de «nombre efectiu d’espècies», que s’entenen millor amb un exemple. Suposem que la distribució d’abundància d’una espècie en una comunitat té una entropia de Shannon de 2,77 (utilitzant logaritmes en base e). Podríem valorar la magnitud d’aquesta xifra, 2,77, construint una comunitat de referència amb la mateixa entropia però que incloguera només un nombre X d’espècies igual de comunes. Descobrir el valor de X és una qüestió d’àlgebra, i en aquest cas el resultat és X = 16 espècies igual de comunes; una comunitat amb 16 espècies igual de comunes té la mateixa entropia que la comunitat real, 2,77. Per tant el «nombre efectiu d’espècies» per a una entropia de Shannon de 2,77 correspon a 16. Si en aquest exemple usem varia­bles en compte de nombres concrets, podem derivar una fórmula general per a convertir l’entropia de Shannon en el nombre efectiu d’espècies; la fórmula de conversió és simplement exp(H), en la qual H és l’entropia de Shannon utilitzant logaritmes naturals.

Podem repetir el procés amb una segona comunitat en la qual l’entropia és 3,46. A primera vista no sembla molt diferent de l’entropia de la primera comunitat, 2,77. No obstant això, fan falta 32 espècies igual de comunes per a aconseguir una entropia de 3,46. Pel que fa a l’entropia de Shannon, la diferència entre la primera comunitat i la segona és igual que la diferència en entropia entre una comunitat de 16 espècies igual de comunes i una de 32. Això demostra com poden semblar d’enganyosos els valors de l’entropia de Shannon per a avaluar els canvis en un ecosistema. Quan convertim les entropies en el nombre efectiu d’espècies, aconseguim un sentit més clar del seu significat. A més, el «nombre efectiu d’espècies» és independent de la base utilitzada per a calcular el logaritme en l’entropia.

Recentment es va descobrir la radiació evolutiva local de noves espècies d’orquídies del gènere Teagueia en l’est d’Equador. Aquest és un exemple de gran diversitat d’espècies amb poca diversitat filogenètica. / © Lou Jost/EcoMinga

Podem utilitzar el mateix mètode per a trobar el nombre efectiu d’espècies a partir de l’índex Gini-Simpson o qualsevol altra entropia generada amb les fórmules mestres mencionades anteriorment. Totes porten a una única fórmula mestra per al nombre efectiu d’espècies, expressat com una funció del mateix paràmetre q que ens va donar el perfil d’entropia d’una comunitat; el paràmetre q determina la sensibilitat del càlcul a l’abundància relativa d’espècies (Taula 1). La gràfica del nombre efectiu d’espècies enfront de q (en què q va des de zero a infinit) és el «perfil de diversitat» de la comunitat. Convertir tots els càlculs tradicionals de complexitat a una mateixa mètrica senzilla, el nombre efectiu d’espècies, ens permet comparar-los directament per a saber més sobre l’estructura d’una comunitat (Figura 1). Ara ja no estem comparant el nombre d’espècies amb el nombre de bits o amb probabilitats, que era com comparar taronges i pomes. I el millor de tot, quan els càlculs tradicionals de complexitat, sensibles a l’abundància, es converteixen al nombre efectiu d’espècies, obeeixen al principi de replicació descrit anteriorment, com la riquesa d’espècies. Això li proporciona algunes (encara que no totes) de les propietats intuïtives de la riquesa d’espècies. Per exemple, el nombre efectiu d’espè­cies permet mesurar la similitud entre comunitats observant la proporció de diversitat mitjana intragrupal amb la diversitat total agregada, la mateixa tècnica que els biòlegs (erròniament) intentaven utilitzar amb els càlculs tradicionals. El bon desenvolupament matemàtic que subjau al nombre efectiu d’espècies també revela com dividir la diversitat en components independents intra i intergrupals, i mostra que aquests components es relacionen amb els càlculs habituals de similitud entre ecosistemes. El nombre efectiu d’espècies, per tant, és la millor eina per a quantificar el concepte de diversitat que utilitzen realment la majoria de biòlegs.

El concepte de diversitat es va des­envolupar per a descriure aspectes fonamentals dels ecosistemes. No obstant això, perquè la disciplina avance, el llenguatge descriptiu també hauria de connectar amb la teoria predictiva. El concepte de diversitat en termes de nombre efectiu d’espècies té connexions profundes amb la majoria de models importants d’ecosistema i població utilitzats pels ecòlegs, com el model neutral de Hubbell (2001). Els valors esperats d’entropia generalitzada i nombre efectiu d’espècies per a q = 0, 1 i 2 són funcions analítiques simples dels paràmetres fonamentals del model de Hubbell (Chao et al., 2015). Això significa que els biòlegs poden predir la diversitat i la semblança compositiva entre ecosistemes a partir de paràmetres fonamentals com la grandària de les poblacions i la taxa d’especiació, en el cas de models idealitzats simples. Els biòlegs encara estan molt lluny de poder predir aquestes qüestions en el desordre dels ecosistemes ­reals, però aquest és un primer pas important.

«En models idealitzats simples, els biòlegs poden predir la diversitat i la semblança compositiva entre ecosistemes»

Ampliar el concepte de diversitat

És perfecte aquest concepte de diversitat? Per descomptat que no. Una de les abstraccions subjacents és que totes les espècies són igual de diferents les unes de les altres. Un grup de cinc espècies de rata té la mateixa diversitat que un grup consistent en una rata, un armadillo, un manatí, un pangolí i una mona, sempre que les abundàncies relatives siguen iguals en ambdós casos. Els càlculs de diversitat estàndard depenen només de les abundàncies relatives de cada espècie, no del seu nivell de diferenciació. No obstant això, el segon grup té molta més història evolutiva i, per tant, molt més valor de conservació. Amb l’aparició de les tècniques de seqüenciació genètica podem calcular objectivament el temps de divergència entre espècies, així doncs el concepte tradicional de diversitat, que era molt simple, s’ha ampliat recentment per a incorporar-hi la història evolutiva única continguda en cada comunitat. Això es va fer en un principi generalitzant els mètodes tradicionals –la riquesa d’espècies, l’entropia de Shannon i, sobretot, l’índex Gini-Simpson– per a incorporar el temps de divergència, però les generalitzacions de les dues últimes van heretar els mateixos problemes d’interpretació que les seues progenitores. Recentment el marc sencer de la diversitat entès com a nombre efectiu d’espècies, amb totes les seues divisions i càlculs de similitud, s’ha generalitzat per a incloure-hi el temps de divergència, i ara hi ha una aproximació matemàticament rigorosa disposada a enfrontar-se a noves qüestions ecològiques que fa unes dècades no podíem ni imaginar (Chao, Chiu i Jost, 2010). També hi ha un treball conti­nuat que intenta incloure les diferències entre espècies (vegeu Chao, Chiu i Jost, 2014), encara que aquestes diferències són molt més difícils de quantificar objectivament que el temps de divergència evolutiva.

A pesar d’aquests avenços en matemàtica de la diversitat, és essencial que ens adonem que la diversitat és només un paràmetre i que el quadre complet requereix paràmetres descriptius addicionals. Per exemple, la majoria dels desenvolupaments fins a la data s’han centrat en càlculs de la diversitat que depenen de les abundàncies relatives. Aquests càlculs funcionen bé per a ecosistemes amb densitats d’individus fixes, com el típic ecosistema boscós en què la composició d’espècies pot canviar entre localitzacions o d’un any a un altre però la densitat és més o menys estable. No obstant això, en alguns ecosistemes la densitat total pot fluctuar ràpidament, com ocorre en algunes comunitats terrestres d’insectes, que creixen breument amb l’aparició massiva d’adults voladors d’espècies d’insectes aquàtics que proliferen en llacs aïllats. Quan s’introdueix una nova espècie superabundant en un ecosistema, els càlculs de diversitat sensibles a les abundàncies cauen dràsticament, perquè es veuen afectats per l’equitativitat de la distribució d’abundàncies relatives. Aquesta disminució en diversitat (per a q > 0) és una descripció exacta de la caiguda sobtada en complexitat; ara és molt probable que qualsevol interacció entre dos individus siga entre conespecífics (de l’espècie superabundant), en compte de ser-ho entre dues espècies distintes. No obstant això, aquest no és el tipus de disminució de la diversitat que hauria de preocupar els ecologistes. Per a saber si hauríem de preocupar-nos quan disminueix la diversitat o no, necessitem informació addicional sobre les abundàncies absolutes. En el cas d’una invasió explosiva d’insectes, la corba d’acumulació d’una espècie (entesa com una funció del treball de mostreig) ens dirà si hi ha alguna cosa de què preocupar-se. La diversitat és un concepte poderós, però no és l’única cosa que hem de saber sobre un ecosistema!