El banyista de Siracusa

Il·lustració: Hugo Salais

De menuda, el meu referent de savi boig amb cabells blancs era Arquimedes. El meu llibre de capçalera llavors, el Dime quién es, explicava la història de la seua boja carrera, nu, cridant «Eureka!» per tota Siracusa, després de trobar la solució al problema que l’obsessionava: si la corona del rei Hieró era d’or o l’orfebre l’havia enganyat daurant un altre metall. Potser per decòrum de llibre infantil, la il·lustració el mostrava poc abans, a la banyera, mirant l’augment del nivell de l’aigua després d’entrar-hi. Jo també vaig començar a fixar-me quan em banyava, sense arribar al moment «Equilicuá!», com hauria dit la meua àvia Severiana. Quan, de major, vaig estudiar hidrostàtica, això del nivell de l’aigua en la banyera no em va semblar una observació especialment genial. Què va descobrir Arquimedes realment? I, amb quin propòsit?

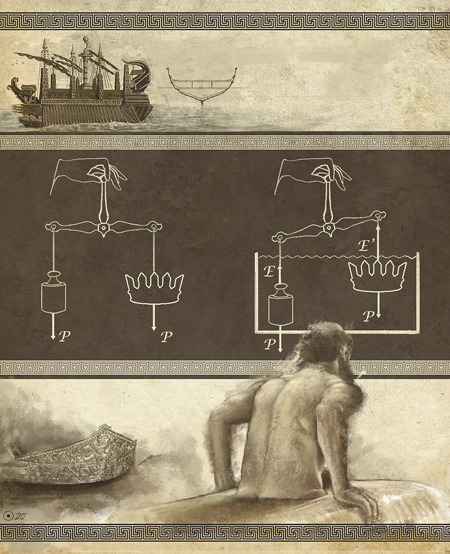
Si sostenim un objecte sobre la mà, sentim la seua força de contacte (igual al pes de l’objecte). Ara submergim mà i objecte (aquest no ha de surar) sota l’aigua i notem que la força de contacte disminueix. Això és degut al fet que apareix l’empenta E, que només depén de la massa d’aigua desplaçada per l’objecte en submergir-lo i és degut al fet que la pressió de l’aigua augmenta amb la profunditat. Sobre dues boles iguals, una de plom i una altra de suro, introduïdes totalment en aigua, es produeix la mateixa empenta. El pes de la bola de suro és menor que E, per tant, en soltar-la, puja i flota (i deixa una part fora de l’aigua). El pes de la de plom és major que E i la bola s’afona. Si transforme la bola de plom en un got o bol buit, el pes no canvia, però ara l’empenta és major: desplaça més massa d’aigua i aconseguisc que flote. D’altra banda, i com il·lustra la figura de la pàgina anterior, dos cossos poden tindre el mateix pes P i, en introduir-los en un fluid, la balança es desequilibra: això significa que els seus volums són diferents (diferents empentes E i E’) i que estan fets de diferents materials.

«L’historiador de la ciència Alexander Koyrè va resumir el treball científic del segle XVI com una comprensió gradual de les obres d’Arquimedes»

Se sap que Arquimedes, igual com altres científics hel·lenístics, va abordar molts problemes físics i matemàtics, i nombrosos projectes tecnològics, com la manus ferrea (garra) que va destruir l’armada romana, l’architronito –canó a vapor recuperat per Leonardo da Vinci–, o el disseny d’engranatges i corrioles, com els que va usar per a avarar el Siracusia, una espècie de Titanic de luxe amb una carena tan gran, per a augmentar l’empenta, que no podia fondejar en quasi cap port. També va supervisar la seua construcció i va dissenyar les catapultes defensives de coberta contra el pirateig.

Galileu Galilei malparlava de Vitruvi (origen de la llegenda de l’«eureka») per banalitzar la sofisticació científica del siracusà. De fet, l’historiador de la ciència Alexander Koyrè va resumir el treball científic del segle XVI com una comprensió gradual de les obres d’Arquimedes. Entre aquestes, el tractat «sobre els cossos flotants» que analitza l’estabilitat de cossos que tenen forma de bol o paraboloide: la forma de qualsevol nau. Basant-se en aquest treball, Galileu va reconstruir el mètode per a determinar la densitat d’un cos, usat també avui dia. Li hauria agradat l’Arquimedes pintat pel seu coetani Josep de Ribera: de rostre mediterrani, eixut i calb, amb ment absorta i somriure maliciós, pensant «Equilicuá!».